题目内容
设函数 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 ,则曲线
,则曲线 在点
在点 处切线的斜率为 ( )
处切线的斜率为 ( )
| A.2 | B. | C.4 | D. |
C
解析试题分析:因为曲线 在点
在点 处的切线方程为
处的切线方程为 ,所以
,所以 因为
因为 ,所以
,所以 即曲线
即曲线 在点
在点 处切线的斜率为4.
处切线的斜率为4.
考点:本小题主要考查导数的几何意义,考查学生的运算能力.
点评:导数的几何意义是高考中常考的内容,求切线方程时,分清是某点处的切线还是过某点的切线.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
若函数 满足
满足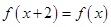 且
且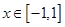 时,
时,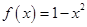 ,函数
,函数 ,则函数
,则函数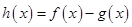 在区间
在区间 内的零点的个数为( )
内的零点的个数为( )
A. | B. | C. | D. |
定义函数 ,其中
,其中 ,且对于
,且对于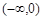 中的任意一个
中的任意一个 都与集合
都与集合 中的
中的 对应,
对应, 中的任意一个
中的任意一个 都与集合
都与集合 中的
中的 对应,则
对应,则 的值为( )
的值为( )
A. | B.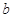 | C.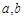 中较小的数 中较小的数 | D.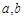 中较大的数 中较大的数 |
对于任意 ,函数
,函数 的值恒大于零,那么
的值恒大于零,那么 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
根据表格中的数据,可以判断方程 必有一个根在区间( )
必有一个根在区间( )
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.78 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
B.(0,1)
C.(1,2)
D.(2,3)
函数 的定义域为{0,1,2,3},那么其值域为( )
的定义域为{0,1,2,3},那么其值域为( )
A. | B.{0,1,2,3} |
C. | D. |
定义在 上的函数
上的函数 满足
满足 ,当
,当 时,
时, ,当
,当 时,
时,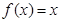 ,则
,则
| A.335 | B.338 | C.1678 | D.2012 |
f (x)= (n∈Z)是偶函数,且y=f(x)在(0,+∞)上是减函数,则n=( ).
(n∈Z)是偶函数,且y=f(x)在(0,+∞)上是减函数,则n=( ).
| A.1 | B.2 | C.1或2 | D.3 |
 满足以下三个条件:①对于任意的
满足以下三个条件:①对于任意的 ,都有
,都有 ;②对于任意的
;②对于任意的 ③函数
③函数 的图象关于y轴对称,则下列结论中正确的是
的图象关于y轴对称,则下列结论中正确的是


