题目内容
 为正方形,
为正方形, 平面
平面 ,
, ,则
,则 与
与 所成角的度数为
所成角的度数为
| A.30° | B.45° | C.60° | D.90° |
C
解析试题分析:以D为坐标原点,DA所在直线为x轴,DC所在线为y轴,DP所在线为z轴,建立空间坐标系,∵点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,令PD=AD=1
∴A(1,0,0),P(0,0,1),B(1,1,0),D(0,0,0)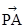 =(1,0,-1),
=(1,0,-1),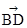 =(-1,-1,0)
=(-1,-1,0)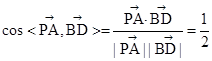 故两向量夹角的余弦值为
故两向量夹角的余弦值为 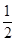 ,即两直线PA与BD所成角的度数为60°.故答案为:60°,选C.
,即两直线PA与BD所成角的度数为60°.故答案为:60°,选C.
考点:本题主要考查了异面直线所角的求法,由于本题中所给的背景建立空间坐标系方便,故采取了向量法求两直线所成角的度数,从解题过程可以看出,此法的优点是不用作辅助线,大大降低了思维难度
点评:解决该试题的关键是宜用向量法来做,以D为坐标原点,建立空间坐标系,求出两直线的方向向量,利用数量积公式求夹角即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知向量 不共线,
不共线, 如果
如果 //
// 那么 ( )
那么 ( )
A. 且c与d反向 且c与d反向 | B. 且c与d反向 且c与d反向 |
C. 且c与d同向 且c与d同向 | D. 且c与d同向 且c与d同向 |
在 所在的平面内有一点P,如果
所在的平面内有一点P,如果 ,那么
,那么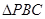 和面积与
和面积与 的面积之比是
的面积之比是
A.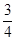 | B. | C. | D. |
在 中,
中, 边的高为
边的高为 ,若
,若 ,
, ,
, ,
, ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
平面向量的集合 到
到 的映射
的映射 由
由 确定,其中
确定,其中 为常向量.若映射
为常向量.若映射 满足
满足 对
对 恒成立,则
恒成立,则 的坐标不可能是 ( )
的坐标不可能是 ( )
A. | B. |
C. | D. |
 、
、 、
、 满足
满足 ,
, ,
,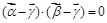 .若对每一确定的
.若对每一确定的 ,
, 的最大值和最小值分别为
的最大值和最小值分别为 、
、 ,则对任意
,则对任意 的最小值是 ( )
的最小值是 ( )
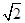
 =2
=2 ,
, ·(
·( +
+ )等于( )
)等于( )

 与圆
与圆 交于
交于 、
、 两点,
两点, 是原点,C是圆上一点,若
是原点,C是圆上一点,若 ,则
,则 的值为_______ .
的值为_______ .