题目内容
在 所在的平面内有一点P,如果
所在的平面内有一点P,如果 ,那么
,那么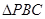 和面积与
和面积与 的面积之比是
的面积之比是
A.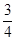 | B. | C. | D. |
A
解析试题分析:因为 
所以 ,即
,即 
所以 A, P, C在同一直线,△PBC与 △ABC高一样,
所以面积比=  =3:4,故选A。
=3:4,故选A。
考点:本题主要考查平面向量的线性运算,共线向量。
点评:简单题,研究三角形面积之比,必定要研究三角形的边长关系,本题从证明三点共线、共线向量入手,达到明确边长关系、高的关系之目的。

练习册系列答案
相关题目
设 ,向量
,向量 ,b=(3,—2),且
,b=(3,—2),且 则|a-b|=( )
则|a-b|=( )
| A.5 | B. | C.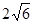 | D.6 |
已知O是 内部一点,
内部一点, 则
则 的面积为( )
的面积为( )
A. | B. | C. | D. |
已知向量 ,
,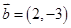 ,若向量
,若向量 满足
满足 ,
, ,则
,则 ="(" )
="(" )
A. | B.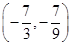 | C. | D. |
若平面向量 满足
满足 =
= ,
, ,
, ,则平面向量
,则平面向量 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
已知 为互相垂直的单位向量,向量a
为互相垂直的单位向量,向量a ,b
,b ,且a与a+
,且a与a+ b的夹角为锐角,则实数
b的夹角为锐角,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
 为正方形,
为正方形, 平面
平面 ,
, ,则
,则 与
与 所成角的度数为
所成角的度数为
| A.30° | B.45° | C.60° | D.90° |
已知向量 且
且 ,则
,则 等于
等于
A. | B.- | C. | D.- |
 、
、 满足
满足 ,
, ,且
,且 (
( ),则
),则 .
.