题目内容
平面向量的集合 到
到 的映射
的映射 由
由 确定,其中
确定,其中 为常向量.若映射
为常向量.若映射 满足
满足 对
对 恒成立,则
恒成立,则 的坐标不可能是 ( )
的坐标不可能是 ( )
A. | B. |
C. | D. |
D
解析试题分析:由题意可知,令 ,则有f(
,则有f( =
= =
= =
=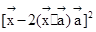
=
而利用向量的模的定义可知选项B,C中向量的模为1,选项A为零向量,
故选D
考点:本试题主要考查了向量的运算法则及向量的运算律。
点评:解决该试题的关键是通过赋值列出关于向量的方程,通过向量的运算法则化简方程,得到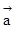 满足的条件。
满足的条件。

练习册系列答案
相关题目
若平面向量 满足
满足 =
= ,
, ,
, ,则平面向量
,则平面向量 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
 为正方形,
为正方形, 平面
平面 ,
, ,则
,则 与
与 所成角的度数为
所成角的度数为
| A.30° | B.45° | C.60° | D.90° |
在 中,
中, 为边
为边 中线
中线 上的一点,若
上的一点,若 ,则
,则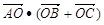 的( )
的( )
| A.最大值为8 | B.最大值为4 | C.最小值-4 | D.最小值为-8 |
已知向量 且
且 ,则
,则 等于
等于
A. | B.- | C. | D.- |
 ,点
,点 为
为 所表示的平面区域内任意一点,
所表示的平面区域内任意一点, ,
, 为坐标原点,
为坐标原点, 为
为 的最小值,则
的最小值,则



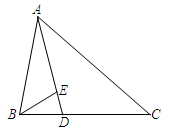
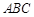 中,已知
中,已知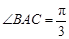 ,
,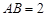 ,
,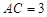 ,
,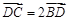 ,
,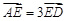 ,则
,则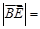 .
.
 的直线与两坐标轴的正半轴交于
的直线与两坐标轴的正半轴交于 、
、 两点,
两点, 为坐标原点,
为坐标原点, ,则四边形
,则四边形 周长的最小值等于
周长的最小值等于



