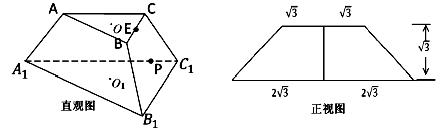题目内容
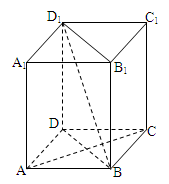
如图,直角梯形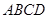 与等腰直角三角形
与等腰直角三角形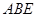 所在的平面互相垂直.
所在的平面互相垂直.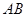 ∥
∥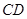 ,
,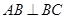 ,
,
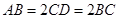 ,
,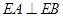 .
.
(1)求证: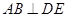 ;
;
(2)求直线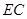 与平面
与平面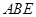 所成角的正弦值;
所成角的正弦值;
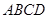 与等腰直角三角形
与等腰直角三角形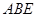 所在的平面互相垂直.
所在的平面互相垂直.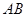 ∥
∥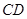 ,
,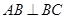 ,
,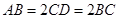 ,
,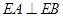 .
.(1)求证:
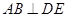 ;
;(2)求直线
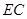 与平面
与平面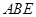 所成角的正弦值;
所成角的正弦值; (1)取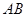 中点
中点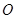 ,连结
,连结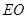 ,
,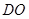 .证得
.证得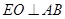 ,由四边形
,由四边形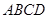 为直角梯形,得到
为直角梯形,得到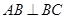 ,证得
,证得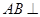 平面
平面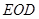 .推出
.推出 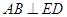 .
.
(2)直线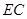 与平面
与平面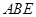 所成角的正弦值为
所成角的正弦值为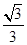 .
.
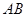 中点
中点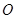 ,连结
,连结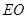 ,
,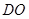 .证得
.证得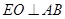 ,由四边形
,由四边形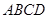 为直角梯形,得到
为直角梯形,得到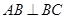 ,证得
,证得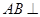 平面
平面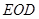 .推出
.推出 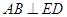 .
.(2)直线
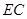 与平面
与平面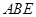 所成角的正弦值为
所成角的正弦值为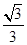 .
. 试题分析:(1)证明:取
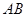 中点
中点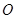 ,连结
,连结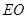 ,
,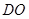 .
.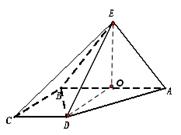
因为
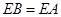 ,所以
,所以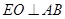 2分
2分因为四边形
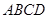 为直角梯形,
为直角梯形,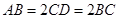 ,
,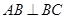 ,
,所以四边形
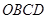 为正方形,所以
为正方形,所以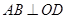 . 4分
. 4分所以
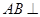 平面
平面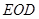 .
. 所以
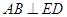 . 6分
. 6分 (2)解法1:因为平面
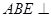 平面
平面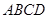 ,且
,且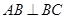
所以BC⊥平面
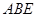 8分
8分则
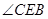 即为直线
即为直线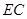 与平面
与平面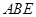 所成的角 9分
所成的角 9分设BC=a,则AB=2a,
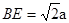 ,所以
,所以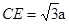
则直角三角形CBE中,
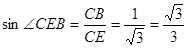 。11分
。11分即直线
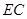 与平面
与平面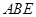 所成角的正弦值为
所成角的正弦值为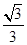 . 。12分
. 。12分解法2:因为平面
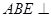 平面
平面 ,且
,且 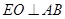 ,
,
所以
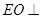 平面
平面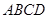 ,所以
,所以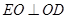 .
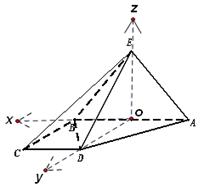
. 由
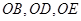 两两垂直,建立如图所示的空间直角坐标系
两两垂直,建立如图所示的空间直角坐标系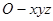 . 因为三角形
. 因为三角形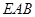 为等腰直角三角形,所以
为等腰直角三角形,所以 ,设
,设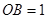 ,
,则
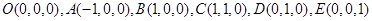 .
.所以
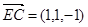 ,平面
,平面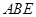 的一个法向量为
的一个法向量为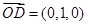 .
.设直线
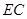 与平面
与平面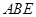 所成的角为
所成的角为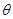 ,
,所以
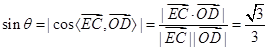 ,
, 即直线
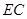 与平面
与平面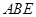 所成角的正弦值为
所成角的正弦值为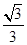 .(参照解法1给步骤分) 12分
.(参照解法1给步骤分) 12分点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离及体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用向量则能简化证明过程。本题给出了两种解法,便于比较借鉴。

练习册系列答案
相关题目
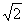 .
.
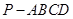 中,
中,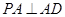 ,
,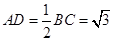 ,
,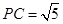 .
.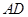 ∥
∥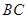 ,
,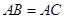 .
.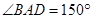
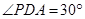 .
.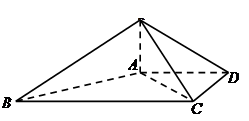
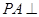 平面
平面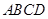 ;
;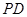 上是否存在一点
上是否存在一点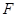 ,使直线
,使直线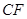 与平面
与平面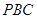 成角正弦值等于
成角正弦值等于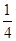 ,若存在,指出
,若存在,指出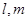 ,平面
,平面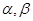 ,且
,且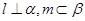 ,给出四个命题: ①若
,给出四个命题: ①若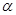 ∥
∥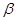 ,则
,则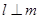 ;②若
;②若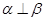 ,则
,则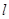 ∥m;④若
∥m;④若 AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.
AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.
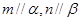 且
且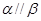 ,则
,则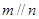 ;②若
;②若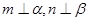 且
且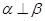 ,则
,则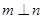 ;
; 且
且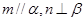 且
且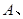 ①②
①② 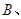 ③④
③④ 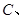 ①④
①④ 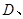 ②③
②③ ,
, 是两条不同的直线,
是两条不同的直线, ,
, 是两个不同的平面,则下列正确命题的序号
是两个不同的平面,则下列正确命题的序号 ,
, , 则
, 则  ; ②.若
; ②.若 ,则
,则  ;
; ,
, ; ④.若
; ④.若  ,
, .
.