题目内容
11.若实数x,y满足|x|+|y|≤1,则|4x+y-2|+|3-x-2y|的最小值是$\frac{4}{3}$.分析 分情况讨论目标函数化简,画出约束条件所表示的可行域,结合图形找出最优解,可求出目标函数的最小值.
解答 解:(1)当$\left\{\begin{array}{l}{4x+y-2≥0}\\{3-x-2y≥0}\end{array}\right.$时,作出满足约束条件的可行域如图,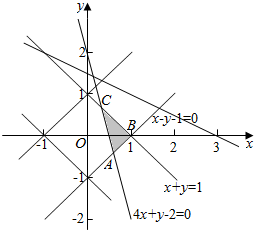
令z=|4x+y-2|+|3-x-2y|=3x-y+1,则y=3x+1-z,
∴y=3x+1-z过点C时,1-z取得最大值,z取得最小值.
解方程组$\left\{\begin{array}{l}{x+y=1}\\{4x+y-2=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=\frac{2}{3}}\end{array}\right.$.∴z=3x-y+1=$\frac{4}{3}$.
(2)当$\left\{\begin{array}{l}{4x+y-2<0}\\{3-x-2y≥0}\end{array}\right.$时,作出满足约束条件的可行域如图,
令z=|4x+y-2|+|3-x-2y|=-5x-3y+5,
则y=-$\frac{5}{3}x$+$\frac{5-z}{3}$,
∴y=-$\frac{5}{3}x$+$\frac{5-z}{3}$经过点C时,$\frac{5-z}{3}$取得最大值,z取得最小值,
由(1)知,C($\frac{1}{3}$,$\frac{2}{3}$),∴z=-5x-3y+5=$\frac{4}{3}$. (3)当3-x-2y<0时,不存在符合条件的可行域,
(3)当3-x-2y<0时,不存在符合条件的可行域,
综上,|4x+y-2|+|3-x-2y|的最小值是$\frac{4}{3}$.
∴故答案为:$\frac{4}{3}$.
点评 本题考查了简单线性规划的应用,正确作出平面区域是关键.

| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
| A. | 锐角三角形 | B. | 钝角三角形 | ||
| C. | 等腰且钝角三角形 | D. | 等腰三角形 |
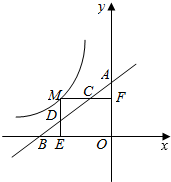 如图,M为曲线y=-$\frac{4}{x}$上的一点.过点M作x轴、y轴的垂线.垂足分别为E、F.分别交直线y=$\frac{\sqrt{3}}{3}$x+m于点D、C两点.若直线y=$\frac{\sqrt{3}}{3}$x+m与y轴交于点A.与x轴相交于点B;
如图,M为曲线y=-$\frac{4}{x}$上的一点.过点M作x轴、y轴的垂线.垂足分别为E、F.分别交直线y=$\frac{\sqrt{3}}{3}$x+m于点D、C两点.若直线y=$\frac{\sqrt{3}}{3}$x+m与y轴交于点A.与x轴相交于点B;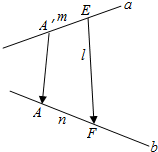 如图,两条异面直线a,b所成的角为θ,在直线a,b上分别取点A′,E和点A,F,使AA′⊥a,且AA′⊥b(AA′称为异面直线a,b的公垂线),已知A′E=m,AF=n,EF=l,求公垂线AA′的长.
如图,两条异面直线a,b所成的角为θ,在直线a,b上分别取点A′,E和点A,F,使AA′⊥a,且AA′⊥b(AA′称为异面直线a,b的公垂线),已知A′E=m,AF=n,EF=l,求公垂线AA′的长.