题目内容
1.已知平面α,β,γ,且α⊥γ,β∥α,求证:β⊥γ.分析 平面α与平面γ相交,设交线为m,在平面α内作直线a⊥m,在平面β内任取一点O,由直线a和点O确定平面M,设M∩β于b,由面面平行的判定定理,能证明β⊥γ.
解答 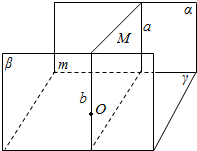 证明:如图,∵平面α⊥平面γ,
证明:如图,∵平面α⊥平面γ,
∴平面α与平面γ相交,设交线为m,
在平面α内作直线a⊥m,∵平面α⊥平面γ,∴a⊥γ,
在平面β内任取一点O,由直线a和点O确定平面M,设M∩β于b,
∵平面α∥平面β,由面面平行的判定定理,得a∥b,
∵a∥b,a⊥γ,∴b⊥γ
又∵b?β,
∴平面β⊥平面γ.
点评 本题考查面面垂直的证明,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
9.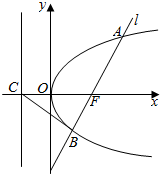 设抛物线y2=2px(p>0)的焦点为F,其准线和x轴的交点为C,经过点F的直线l与抛物线相交于A、B两点,若CB⊥AB,则|AF|-|BF|=( )
设抛物线y2=2px(p>0)的焦点为F,其准线和x轴的交点为C,经过点F的直线l与抛物线相交于A、B两点,若CB⊥AB,则|AF|-|BF|=( )
 设抛物线y2=2px(p>0)的焦点为F,其准线和x轴的交点为C,经过点F的直线l与抛物线相交于A、B两点,若CB⊥AB,则|AF|-|BF|=( )
设抛物线y2=2px(p>0)的焦点为F,其准线和x轴的交点为C,经过点F的直线l与抛物线相交于A、B两点,若CB⊥AB,则|AF|-|BF|=( )| A. | $\frac{P}{2}$ | B. | -$\frac{P}{2}$ | C. | 2P | D. | -2P |
16.函数y=$\sqrt{3x-1}$+lg(1-x)的定义域为( )
| A. | (0,$\frac{1}{3}$) | B. | [0,1) | C. | [$\frac{1}{3}$,1) | D. | [1,3) |