将函数y=sin2x的图象向右平移$\frac{π}{4}$个单位.再向上平移一个单位.所得函数图象对应的解析式为( )A．y=2sin2xB．y=2cos2xC．y=sin+1D．y=-cos2x 题目和参考答案——青夏教育精英家教网—

题目内容

11．将函数y=sin2x的图象向右平移$\frac{π}{4}$个单位，再向上平移一个单位，所得函数图象对应的解析式为（　　）

A．

y=2sin²x

B．

y=2cos²x

C．

y=sin（2x-$\frac{π}{4}$）+1

D．

y=-cos2x

分析由条件利用诱导公式、函数y=Asin（ωx+φ）的图象变换规律，可得结论．

解答解：将函数y=sin2x的图象向右平移$\frac{π}{4}$个单位，可得函数y=sin2（x-$\frac{π}{4}$）=-cos2x 的图象，
再向上平移一个单位，所得函数图象对应的解析式y=-cos2x+1=2sin²x，
故选：A．

点评本题主要考查诱导公式的应用，函数y=Asin（ωx+φ）的图象变换规律，属于基础题．

练习册系列答案

2．已知函数f（x）=（ax²+x-1）e^x，g（x）=$\frac{1}{3}$x³+$\frac{1}{2}$x²+m．
（Ⅰ）当a＜0时，求函数f（x）的单调区间；
（Ⅱ）当a=-1时，若函数h（x）=f（x）-g（x）有3个不同的零点，求实数m的取值范围．

19．已知A，B，C，D是以O为球心的球面上的四点，AB，AC，AD两两互相垂直，且AB=3，AC=4，AD=$\sqrt{11}$，则球的半径为（　　）

	A．	若向量$\overrightarrow{a}$∥$\overrightarrow{b}$，则存在唯一实数λ使$\overrightarrow{a}$=λ$\overrightarrow{b}$
	B．	“若θ=$\frac{π}{3}$，则cosθ=$\frac{1}{2}$”的否命题为“若θ≠$\frac{π}{3}$，则cosθ≠$\frac{1}{2}$”
	C．	已知向量$\overrightarrow{a}$、$\overrightarrow{b}$为非零向量，则“$\overrightarrow{a}$、$\overrightarrow{b}$的夹角为钝角”的充要条件是“$\overrightarrow{a}$$•\overrightarrow{b}$＜0”
	D．	若命题p：?x∈R，x²-x+1＜0，则￢p：?x∈R，x²-x+1＞0

16．已知A={x|-x²+3x-2＞0}，B={x|x²-（a+1）x+a≤0}
（Ⅰ）求B；
（Ⅱ）若A?B时，求实数a的取值范围．

5．在△ABC中，角A、B、C所对的边为a、b、c，且A=120°，b=5，c=6，则a=9．

2．在直角坐标系xOy中，向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$的方向和长度如图所示，分别求它们的坐标．

3．

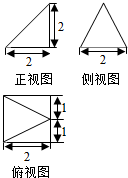已知某几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体得体积是（　　）cm²．

试题分类