题目内容
【题目】为了解学生寒假期间学习情况，学校对某班男、女学生学习时间进行调查，学习时间按整小时统计，调查结果绘成折线图如下：
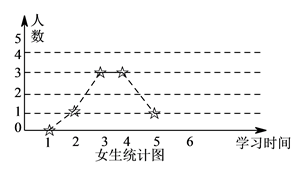
（I）已知该校有 
名学生，试估计全校学生中，每天学习不足 
小时的人数．
（II）若从学习时间不少于 小时的学生中选取 人，设选到的男生人数为 
，求随机变量 的分布列．
（III）试比较男生学习时间的方差 
与女生学习时间方差 
的大小．（只需写出结论）．
【答案】解：由折线图可得共抽取了20人，其中男生中学习时间不足 
小时的有12人，女生中学习时间不足 小时的有8人。
∴可估计全校中每天学习不足 小时的人数为： 
人．
（II）学习时间不少于 本的学生共 
人，其中男学生人数为 人，故 
的所有可能取值为 
， 
， 
， 
， ．
由题意可得 
；
；
；
；
．
所以随机变量 的分布列为
|
|
|
|
|
|
|
|
|
|
|
|
∴均值 
（Ⅲ）由折线图可得 
【解析】(1)根据题意由折线图可估算出每天学习不足 4 小时的人数。(2)由已知得出随机变量 X 的所有可能取值，结合概率的定义分别求出各个值的概率列表即可，再利用均值的公式代入数值求出即可。(3)由图像可得到样本估算结果进而得到结论。
【考点精析】根据题目的已知条件，利用用样本的数字特征估计总体的数字特征的相关知识可以得到问题的答案，需要掌握用样本估计总体时，如果抽样的方法比较合理，那么样本可以反映总体的信息，但从样本得到的信息会有偏差．在随机抽样中，这种偏差是不可避免的．
练习册系列答案
相关题目
