题目内容
在△ABC中,角A、B、C的对边分别为a、b、c.若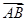 ·
·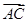 =
=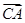 ·
·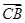 =k(k∈R).
=k(k∈R).
(1)判断△ABC的形状;
(2)若k=2,求b的值.
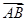 ·
·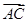 =
=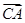 ·
·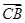 =k(k∈R).
=k(k∈R).(1)判断△ABC的形状;
(2)若k=2,求b的值.
(1)等腰三角形 (2)2
解:(1)∵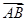 ·
·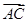 =cbcosA,
=cbcosA,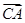 ·
·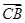 =bacosC,
=bacosC,
∴bccosA=abcosC,
根据正弦定理,
得sinCcosA=sinAcosC,
即sinAcosC-cosAsinC=0,
sin(A-C)=0,
∴A=C,即a=c.
则△ABC为等腰三角形.
(2)由(1)知a=c,由余弦定理,得
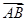 ·
·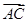 =bccosA=bc·
=bccosA=bc·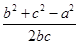 =
=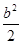 .
.
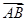 ·
·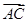 =k=2,
=k=2,
即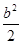 =2,解得b=2.
=2,解得b=2.
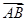 ·
·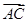 =cbcosA,
=cbcosA,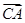 ·
·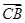 =bacosC,
=bacosC,∴bccosA=abcosC,
根据正弦定理,
得sinCcosA=sinAcosC,
即sinAcosC-cosAsinC=0,
sin(A-C)=0,
∴A=C,即a=c.
则△ABC为等腰三角形.
(2)由(1)知a=c,由余弦定理,得
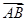 ·
·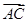 =bccosA=bc·
=bccosA=bc·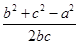 =
=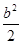 .
.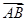 ·
·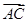 =k=2,
=k=2,即
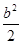 =2,解得b=2.
=2,解得b=2.
练习册系列答案
相关题目
 满足:
满足: ,且当
,且当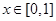 时,
时,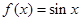 ,其图象与直线
,其图象与直线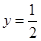 在
在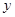 轴右侧的交点按横坐标从小到大依次记为
轴右侧的交点按横坐标从小到大依次记为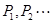 ,则
,则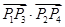 等于 .
等于 . =(2,4),
=(2,4), =(1,3),则
=(1,3),则 ·
· =( )
=( )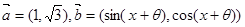 ,若函数
,若函数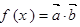 为偶函数,则
为偶函数,则 的值可能是( )
的值可能是( )

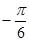

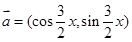 ,
,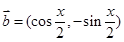 ,且
,且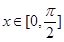 .则函数
.则函数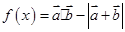 的最小值是 ( )
的最小值是 ( ) 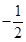
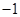
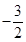

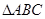 中,
中,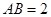 ,
,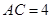 ,且
,且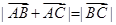 ,则
,则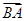 在
在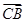 方向上的投影为 .
方向上的投影为 .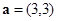 ,
,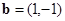 ,若
,若 ,则实数
,则实数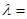 .
.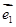 与
与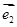 的夹角为
的夹角为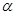 ,且
,且 ,向量
,向量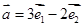 与
与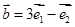 的夹角为
的夹角为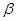 ,则
,则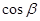 =
= 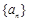 是等差数列,
是等差数列, 为其前n项和,若
为其前n项和,若 , O为坐标原点,点
, O为坐标原点,点 、
、 ,则
,则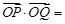 ( )
( )