题目内容
【题目】如图,在三棱柱![]() 中,
中, ![]() 侧面
侧面![]() 底面
底面![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析: (1)由四边形![]() 为菱形,得对角线
为菱形,得对角线![]() ,由侧面
,由侧面![]() 底面
底面![]() ,得
,得![]() 侧面
侧面![]() B1,从而
B1,从而![]() 1,由此能证明
1,由此能证明![]() 平面
平面![]() ;
;
(2)由勾股定理得![]() ,由菱形
,由菱形![]() 中
中![]() ,得
,得![]() 为正三角形,以菱形
为正三角形,以菱形![]() 的对角线交点
的对角线交点![]() 为坐标原点
为坐标原点![]() 方向为
方向为![]() 轴,
轴, ![]() 方向为
方向为![]() 轴,过
轴,过![]() 且与
且与![]() 平行的方向为
平行的方向为![]() 轴建立如图空间直角坐标系,分别求出平面
轴建立如图空间直角坐标系,分别求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,由此能求出二面角
的法向量,由此能求出二面角![]() 的余弦值.
的余弦值.
试题解析:(1)证明:在侧面![]() 中,
中,
![]() ,
,
![]() 四边形
四边形![]() 为菱形,
为菱形,
![]() 对角线
对角线![]() .
.
![]() 侧面
侧面![]() 底面
底面![]() ,
,
![]() 侧面
侧面![]() ,
,
![]() .
.
又![]() ,
,
![]() 平面
平面![]() .
.
(2)在![]() 中,
中, ![]() ,
,
又菱形![]() 中,
中, ![]() ,
,
![]() 为正三角形.
为正三角形.
如图,以菱形![]() 的对角线交点
的对角线交点![]() 为坐标原点
为坐标原点![]() 方向为
方向为![]() 轴,
轴, ![]() 方向为
方向为![]() 轴,过
轴,过![]() 且与
且与![]() 平行的方向为
平行的方向为![]() 轴建立如图空间直角坐标系,
轴建立如图空间直角坐标系,
则![]()
![]() ,
,
设![]() 为平面
为平面![]() 的方向量,则
的方向量,则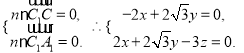
令![]() ,得
,得![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
又![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
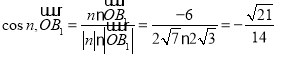 .
.
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目


