题目内容
【题目】已知函数![]() (其中
(其中![]() 为自然对数的底,
为自然对数的底, ![]() )的导函数为
)的导函数为![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(2)设点![]() ,
, ![]() 是函数
是函数![]() 图象上两点,若对任意的
图象上两点,若对任意的![]() ,割线
,割线![]() 的斜率都大于
的斜率都大于![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:(1)由![]()
![]() ,记
,记![]() ,问题转化为函数
,问题转化为函数![]() 的图象与x轴的交点个数问题;(2)对任意的
的图象与x轴的交点个数问题;(2)对任意的![]() ,割线
,割线![]() 的斜率都大于
的斜率都大于![]() ,即
,即![]() ,记
,记![]()
![]() ,研究函数
,研究函数![]() 的单调性与最值即可.
的单调性与最值即可.
试题解析:
(1)![]() 时,由
时,由![]()
![]() ,记
,记![]() ,
,
![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,所以当
,所以当![]() 时,
时, ![]() 取得极小值
取得极小值![]() ,
,
①当![]() 即
即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上无零点;
上无零点;
②当![]() 即
即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有一个零点;
上有一个零点;
③当![]() 即
即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有两个零点;
上有两个零点;
(2)![]() ,
,
![]() ,
, ![]() ,
,
依题意:对任意的![]() ,都有
,都有![]() ,
,
即![]() ,
,
记![]()
![]() ,
, ![]() ,
,
记![]() ,则
,则![]() . 记
. 记![]() ,
,
则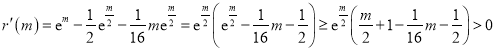 ,
,
所以![]() 时,
时, ![]() 递增,所以
递增,所以![]() ,
,
①当![]() 即
即![]() 时,
时, ![]() ,即
,即![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]() ,得到
,得到![]() ,从而
,从而![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以![]() 恒成立;
恒成立;
②当![]() 即
即![]() 时,因为
时,因为![]() 时,
时, ![]() 递增,所以
递增,所以![]() ,
,
所以存在![]() ,使得
,使得![]() 时,
时, ![]() 即
即![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递减,所以
上单调递减,所以![]() 时,
时, ![]() 即
即![]() ,
,
所以![]() 时,
时, ![]() 在区间
在区间![]() 上单调递减,所以
上单调递减,所以![]() 时,
时, ![]() ,从而
,从而![]() 不恒成立。综上:实数
不恒成立。综上:实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
【题目】大型活动即将举行,为了做好接待工作,组委会招募了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有![]() 人和
人和![]() 人喜爱运动,其余人不喜爱运动.
人喜爱运动,其余人不喜爱运动.
(1)根据以上数据完成以下![]() 列联表:
列联表:
喜爱运动 | 不喜爱运动 | 总计 | |
男志愿者 | |||
女志愿者 | |||
总计 |
(2)根据列联表判断能否有![]() ℅的把握认为性别与喜爱运动有关?
℅的把握认为性别与喜爱运动有关?
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)