题目内容
11．若${（1+\sqrt{3}）^5}=a+b\sqrt{3}$（a，b为有理数），则a+b=120．分析 由题意，${（1+\sqrt{3}）}^{5}$=a+b$\sqrt{3}$的展开式中所有实数项的和为a，所有无理数项中$\sqrt{3}$的系数的和为b，由此求得a，b的值，即可求出a+b得到答案．
解答 解：由题意若${（1+\sqrt{3}）}^{5}$=a+b$\sqrt{3}$（a，b为有理数），由二项式定理得，
a=C50+C52×3+C54×9=76，
b=C51+C53×3+C55×9=44，
∴a+b=120，
故答案为：120．
点评 本题考查二项式定理的应用，熟练掌握二项式定理，理解方程若${（1+\sqrt{3}）}^{5}$=a+b$\sqrt{3}$（a，b为有理数）的意义是解题的关键，理解a，b的意义是本题的难点，也是求解本题的切入点，解题时能把这样的切入点找出来，解题就成功了一半，属于中档题．
练习册系列答案
相关题目
2．若x，y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$，则z=2x+y的最大值是（ ）
| A． | 3 | B． | $\frac{3}{2}$ | C． | 4 | D． | 5 |
6．把函数y=sinx图象上各点的横坐标缩短到原来的$\frac{1}{2}$倍（纵坐标不变）后，再将图象向左平移$\frac{π}{4}$个单位，那么所得图象的一条对称轴方程为（ ）
| A． | $x=-\frac{π}{2}$ | B． | $x=-\frac{π}{4}$ | C． | $x=\frac{π}{8}$ | D． | $x=\frac{π}{4}$ |
3．已知实数a1，a2，a3，a4，a5构成等比数列，其中a1=2，a5=32，则公比q的值为（ ）
| A． | 2 | B． | -2 | C． | 2或-2 | D． | 4 |
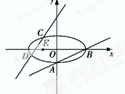如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{\sqrt{6}}{3}$，过点A（0，-b）和B（a，0）的直线与原点的距离为$\frac{\sqrt{3}}{2}$．已知定点E（-1，0），若直线y=kx+2（k≠0）与椭圆交于C，D两点．存在k的值，使以CD为直径的圆过E点，则k=（ ）