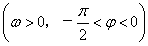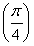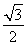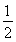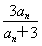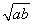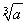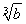题目内容
设a、b、c均为大于1的正数,且ab=10,求证:logac+logbc≥4lgc.
见解析
【解析】(分析法)由于a>1,b>1,c>1,故要证明logac+logbc≥4lgc,只要证明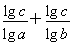 ≥4lgc,即
≥4lgc,即 ≥4,因为ab=10,故lga+lgb=1.只要证明
≥4,因为ab=10,故lga+lgb=1.只要证明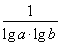 ≥4,由于a>1,b>1,故lga>0,lgb>0,所以0<lgalgb≤
≥4,由于a>1,b>1,故lga>0,lgb>0,所以0<lgalgb≤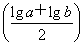 2=
2=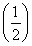 2=
2=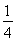 ,即
,即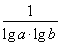 ≥4成立.所以原不等式成立.
≥4成立.所以原不等式成立.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目