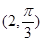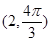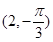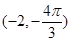题目内容
(1) 已知曲线C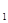 :
: (t为参数), C
(t为参数), C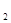 :
: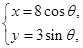 (
(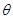 为参数)。化C
为参数)。化C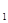 ,C
,C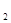 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)求两个圆ρ=4cosθ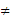 0, ρ=4sinθ的圆心之间的距离,并判定两圆的位置关系。
0, ρ=4sinθ的圆心之间的距离,并判定两圆的位置关系。
 :
: (t为参数), C
(t为参数), C :
: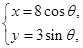 (
(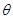 为参数)。化C
为参数)。化C ,C
,C 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;(2)求两个圆ρ=4cosθ
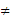 0, ρ=4sinθ的圆心之间的距离,并判定两圆的位置关系。
0, ρ=4sinθ的圆心之间的距离,并判定两圆的位置关系。求解极坐标与参数方程问题,要能够熟练应用相应公式和方法将其转化为直角坐标方程,对于所有问题都可以应用转化思想,化陌生为熟悉,将问题转化为直角坐标方程问题进行解决
(1)(5分)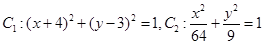
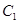 为圆心是
为圆心是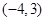 ,半径是1的圆。
,半径是1的圆。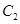 为中心是坐标原点,焦点在
为中心是坐标原点,焦点在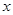 轴上,长半轴长是8,短半轴长是3的椭圆。
轴上,长半轴长是8,短半轴长是3的椭圆。
(2)(5分)解: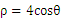 两边同乘以
两边同乘以 得
得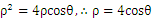 可化为
可化为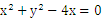 即
即 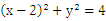
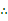 表示的是以
表示的是以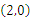 为圆心,半径为2的圆。
为圆心,半径为2的圆。
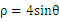 两边同乘以
两边同乘以 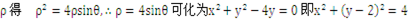
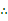 表示的是以
表示的是以 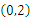 为圆心,半径为2的圆。
为圆心,半径为2的圆。
两员的圆心距为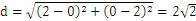 ,两圆半径之和为4,之差为0,
,两圆半径之和为4,之差为0,
所以两圆相交。
(1)(5分)
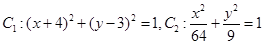
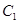 为圆心是
为圆心是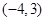 ,半径是1的圆。
,半径是1的圆。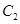 为中心是坐标原点,焦点在
为中心是坐标原点,焦点在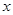 轴上,长半轴长是8,短半轴长是3的椭圆。
轴上,长半轴长是8,短半轴长是3的椭圆。 (2)(5分)解:
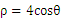 两边同乘以
两边同乘以 得
得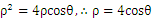 可化为
可化为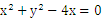 即
即 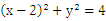
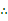 表示的是以
表示的是以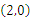 为圆心,半径为2的圆。
为圆心,半径为2的圆。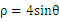 两边同乘以
两边同乘以 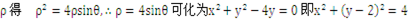
 表示的是以
表示的是以 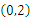 为圆心,半径为2的圆。
为圆心,半径为2的圆。两员的圆心距为
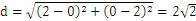 ,两圆半径之和为4,之差为0,
,两圆半径之和为4,之差为0,所以两圆相交。

练习册系列答案
相关题目
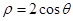 ,则该圆的圆心到直线
,则该圆的圆心到直线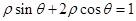 的距离是______________________。
的距离是______________________。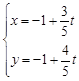 (为参数),曲线
(为参数),曲线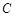 的极坐标方程为
的极坐标方程为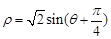 .
.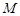 ,
,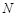 两点,求
两点,求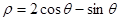 ,则该圆的半径为________.
,则该圆的半径为________.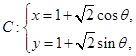 (
(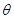 为参数)的极坐标方程为 .
为参数)的极坐标方程为 .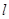 的极坐标方程为
的极坐标方程为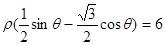 ,圆C的参数方程为
,圆C的参数方程为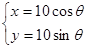 ,求直线
,求直线 到圆
到圆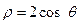 的圆心的距离为
的圆心的距离为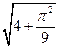
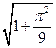
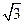
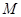 的极坐标是
的极坐标是 ,则点
,则点

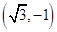
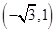
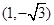 ,则点P的极坐标为( )
,则点P的极坐标为( )