题目内容
选修4-4 坐标系与参数方程已知曲线C的极坐标方程为:
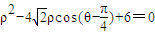 ,
,(Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)设(x,y)是曲线C上任意一点,求
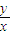 的最大、最小值.
的最大、最小值.
【答案】分析:(Ⅰ)利用极坐标与直角坐标的互化公式即可;
(Ⅱ)设 ,把问题转化为y=kx与圆相切时的直线的斜率问题即可.
,把问题转化为y=kx与圆相切时的直线的斜率问题即可.
解答:解:(Ⅰ)∵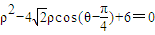 ,∴
,∴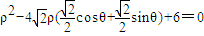 ,
,
∴ρ2-4ρcosθ-4ρsinθ+6=0,
化为普通方程x2+y2-4x-4y+6=0,即(x-2)2+(y-2)2=2,圆心C(2,2),半径r=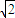 .
.
(Ⅱ)设 ,则y=kx.
,则y=kx.
∵直线y=kx与圆C有公共点,∴圆心C(2,2)到直线y=kx的距离d≤r,即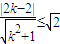 ,化为k2-4k+1≤0,解得
,化为k2-4k+1≤0,解得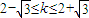 .
.
∴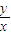 的最大、最小值分别为
的最大、最小值分别为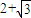 、
、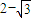 .
.
点评:熟练掌握极坐标与直角坐标的互化公式及直线与圆的位置关系是解题的关键.
(Ⅱ)设
 ,把问题转化为y=kx与圆相切时的直线的斜率问题即可.
,把问题转化为y=kx与圆相切时的直线的斜率问题即可.解答:解:(Ⅰ)∵
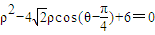 ,∴
,∴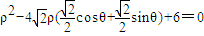 ,
,∴ρ2-4ρcosθ-4ρsinθ+6=0,
化为普通方程x2+y2-4x-4y+6=0,即(x-2)2+(y-2)2=2,圆心C(2,2),半径r=
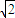 .
.(Ⅱ)设
 ,则y=kx.
,则y=kx.∵直线y=kx与圆C有公共点,∴圆心C(2,2)到直线y=kx的距离d≤r,即
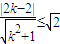 ,化为k2-4k+1≤0,解得
,化为k2-4k+1≤0,解得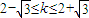 .
.∴
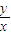 的最大、最小值分别为
的最大、最小值分别为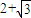 、
、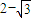 .
.点评:熟练掌握极坐标与直角坐标的互化公式及直线与圆的位置关系是解题的关键.

练习册系列答案
相关题目
 附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)
附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题) .以极点为平面直角坐标系的原点,极轴为x
.以极点为平面直角坐标系的原点,极轴为x 的参数方程是
的参数方程是 ,
, (2)(选修4—5 不等式选讲)已知
(2)(选修4—5 不等式选讲)已知 ,且
,且  ,则
,则 的最小值为 .
的最小值为 . ,
, ,
,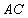 与
与 交于点D,
交于点D, ,
, ,则
,则 .
.