题目内容
已知向量 ,
, ,函数
,函数
(Ⅰ)求 的最大值;
的最大值;
(Ⅱ)在 中,设角
中,设角 ,
, 的对边分别为
的对边分别为 ,若
,若 ,且
,且 ?,求角
?,求角 的大小.
的大小.
(Ⅰ)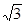 ;(Ⅱ)
;(Ⅱ)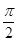 .
.
解析试题分析:(Ⅰ)由向量数量积的定义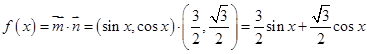 只需将其化为一个角的三角函数就能求出
只需将其化为一个角的三角函数就能求出 的最大值.
的最大值.
(Ⅱ)由(Ⅰ)的结果和正弦定理: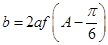
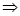
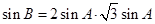 ,
,
又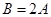 ,所以,
,所以,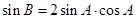 ,由以上两式即可解出
,由以上两式即可解出 ,
,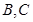 .
.
试题解析:(Ⅰ)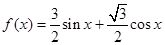 2分
2分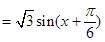 4分(注:也可以化为
4分(注:也可以化为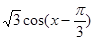 )
)
所以 的最大值为
的最大值为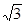 . 6分
. 6分
(注:没有化简或化简过程不全正确,但结论正确,给4分)
(Ⅱ)因为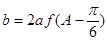 ,由(1)和正弦定理,得
,由(1)和正弦定理,得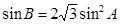 . 7分
. 7分
又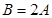 ,所以
,所以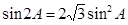 ,即
,即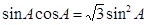 , 9分
, 9分
而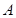 是三角形的内角,所以
是三角形的内角,所以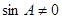 ,故
,故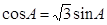 ,
, , 11分
, 11分
所以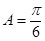 ,
,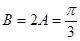 ,
,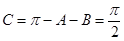 . 12分
. 12分
考点:1.正弦定理;2、两角和与差的在角函数公式、倍角公式;3、三角函数的性质.

练习册系列答案
相关题目
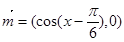 ,
,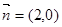 ,
,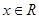 ,函数
,函数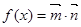 .
.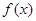 的表达式;
的表达式;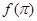 的值;
的值;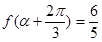 ,
,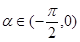 ,求
,求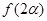 的值.
的值. 中,角
中,角 、
、 、
、 所对应的边为
所对应的边为 、
、 、
、 .
. ,求
,求 ,且
,且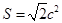 ,求
,求 的值.
的值.  的三个内角A,B,C的对边,
的三个内角A,B,C的对边,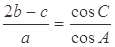
 时,求
时,求 的取值范围.
的取值范围.  ,
, ,设函数
,设函数 .
.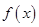 的解析式,并求
的解析式,并求 上的最小值;
上的最小值; 中,
中, 分别是角
分别是角 的对边,
的对边, 为锐角,若
为锐角,若 ,
, ,
, ,求
,求 .
. ,x∈R,且
,x∈R,且 .
. ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.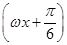 (其中ω>0,x∈R)的最小正周期为10π.
(其中ω>0,x∈R)的最小正周期为10π.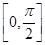 ,f
,f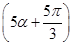 =-
=-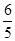 ,f
,f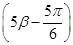 =
=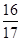 ,求cos(α+β)的值.
,求cos(α+β)的值. tan20°tan40°.
tan20°tan40°. ,n=
,n= ,f(x)=m·n,且f
,f(x)=m·n,且f =
= .
. ,f(3α+π)=
,f(3α+π)= ,f
,f =-
=- ,求cos (α+β)的值.
,求cos (α+β)的值.