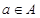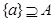题目内容
函数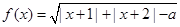 .
.
(1)若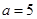 ,求函数
,求函数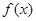 的定义域
的定义域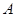 ;
;
(2)设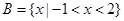 ,当实数
,当实数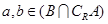 时,证明:
时,证明: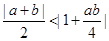 .
.
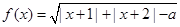 .
.(1)若
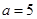 ,求函数
,求函数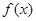 的定义域
的定义域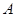 ;
;(2)设
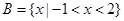 ,当实数
,当实数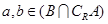 时,证明:
时,证明: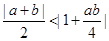 .
.(1)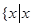 ≤
≤ 或
或 ≥
≥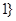 ;(2)参考解析
;(2)参考解析
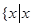 ≤
≤ 或
或 ≥
≥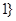 ;(2)参考解析
;(2)参考解析试题分析:(1)由
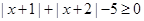 ,绝对值的零点分别为-1和-2.所以通过对实数分三类分别去绝对值可求得结论.
,绝对值的零点分别为-1和-2.所以通过对实数分三类分别去绝对值可求得结论.(2)由(1)可得定义域A.又
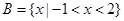 ,当实数
,当实数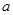 ,
,
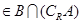 ,所以可以求得实数
,所以可以求得实数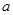 ,
, 的范围.需求证:
的范围.需求证: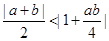 ,等价于平方的大小比较,通过求差法,又
,等价于平方的大小比较,通过求差法,又 即可得到结论.
即可得到结论.(1)由
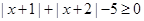
解得
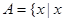 ≤
≤ 或
或 ≥
≥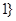 . 5分
. 5分(2)
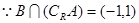 ,又
,又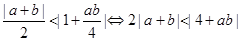 .
.
及
 ,
, .
.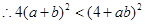 .
. . 10分
. 10分
练习册系列答案
相关题目
在平面直角坐标系中,曲线C:x2-y2=36经过伸缩变换
后,所得曲线的焦点坐标为( )
|
A、(0,±
| ||
B、(±
| ||
C、(0,±
| ||
D、(±
|
 ,
,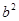 },则
},则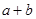 = .
= .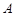 ,如果定义了一种运算“
,如果定义了一种运算“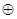 ”,使得集合
”,使得集合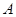 中的元素间满足下列4个条件:
中的元素间满足下列4个条件: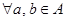 ,都有
,都有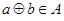 ;
; ,使得对
,使得对 ,都有
,都有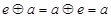 ;
; ,使得
,使得 ;
;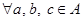 ,都有
,都有 ,
,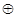 ”构成“对称集”.
”构成“对称集”. ,运算“
,运算“ ,运算“
,运算“ ,运算“
,运算“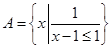 ,
,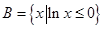 则
则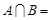 ( )
( )
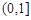
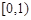
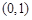
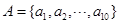 ,定义集合
,定义集合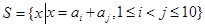 ,记集合
,记集合 中的元素个数为
中的元素个数为 .若
.若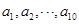 是公差大于零的等差数列,则
是公差大于零的等差数列,则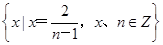 ,则∁UA=________.
,则∁UA=________. ,
,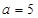 ,则有( )
,则有( )