题目内容
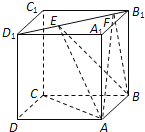
【题目】在直三棱柱ABC﹣A1B1C1中,BC=CC1,AB⊥BC.点M,N分别是CC1,B1C的中点,G是棱AB上的动点.
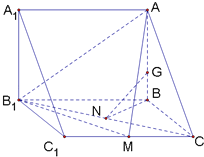
(1)求证:B1C⊥平面BNG;
(2)若CG∥平面AB1M,试确定G点的位置,并给出证明.
【答案】(1)详见解析(2)G是棱AB的中点
【解析】
试题分析:(I)由直三棱柱的性质结合AB⊥BC,得AB⊥平面![]() ,从而
,从而![]() ⊥GB,在等腰△
⊥GB,在等腰△![]() 中,利用中线BN⊥
中,利用中线BN⊥![]() ,根据线面垂直的判定定理,得到
,根据线面垂直的判定定理,得到![]() ⊥平面BNG.(II)当G是棱AB的中点时,CG∥平面
⊥平面BNG.(II)当G是棱AB的中点时,CG∥平面![]() .连接
.连接![]() ,取
,取![]() 的中点H,连接HG、HM、GC,用三角形中位线定理,得到GH∥
的中点H,连接HG、HM、GC,用三角形中位线定理,得到GH∥![]() 且GH=
且GH=![]()
![]() ,在正方形
,在正方形![]() 中证出MC∥
中证出MC∥![]() 且MC=
且MC=![]()
![]() ,所以GH与MC平行且相等,得到四边形HGCM为平行四边形,GC∥HM,最后结合线面平行的判定定理,得到CG∥平面
,所以GH与MC平行且相等,得到四边形HGCM为平行四边形,GC∥HM,最后结合线面平行的判定定理,得到CG∥平面![]()
试题解析:(1):∵在直三棱柱ABC﹣A1B1C1中,BC=CC1=BB1,点N是B1C的中点,
∴BN⊥B1C
∵AB⊥BC,AB⊥BB1,BB1∩BC=B
∴AB⊥平面B1BCC1
∵B1C平面B1BCC1
∴B1C⊥AB,即B1C⊥GB
又∵BN∩BG=B,BN、BG平面BNG
∴B1C⊥平面BNG
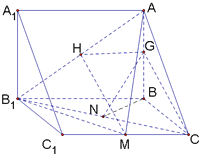
(2)当G是棱AB的中点时,CG∥平面AB1M.
证明如下:
连接AB1,取AB1的中点H,连接HG、HM、GC,
则HG为△AB1B的中位线
∴GH∥BB1,GH=BB1
∵由已知条件,B1BCC1为正方形
∴CC1∥BB1,CC1=BB1
∵M为CC1的中点,
∴![]()
∴MC∥GH,且MC=GH
∴四边形HGCM为平行四边形
∴GC∥HM
又∵GC平面AB1M,HM平面AB1M,
∴CG∥平面AB1M

练习册系列答案
相关题目