题目内容
7.已知函数y=f(x)是定义在R上的偶函数,且对任意实数x,都有f(x+1)=f(x-1)成立,已知当x∈[1,2]时,f(x)=logax(a>0且a≠1).(1)求x∈[-1,1]时,函数f(x)的表达式;
(2)求x∈[2k-1,2k+1](k∈Z)时,函数f(x)的解析式.
分析 (1)由已知中f(x+1)=f(x-1),故可能函数是以2为周期的周期函数,又由函数f(x)是定义在R上的偶函数,结合当x∈[1,2]时,f(x)=logax,我们易得,x∈[-1,1]时,函数f(x)的表达式;
(2)由函数的周期性,我们易得函数的解析式;
解答 解:(1)∵f(x+1)=f(x-1),且f(x)是R上的偶函数,
∴f(x+2)=f(x),
若x∈[-1,0]时,则x+2∈[1,2],
则f(x)=f(x+2)=loga(x+2),x∈[-1,0],
若x∈(0,1],则-x∈[-1,0),
则f(x)=f(-x)=loga(2-x),x∈(0,1],
∴f(x)=$\left\{\begin{array}{l}{log}_{a}(2+x),x∈[-1,0]\\{log}_{a}(2-x),x∈(0,1]\end{array}\right.$
(2)当x∈[2k-1,2k]时,f(x)=f(x-2k)=loga(2+x-2k),
同理,当x∈(2k,2k+1]时,f(x)=f(x-2k)=loga(2-x+2k),
∴f(x)=$\left\{\begin{array}{l}{log}_{a}(2+x-2k),x∈[2k-1,2k]\\{log}_{a}(2-x+2k),x∈(2k,2k+1]\end{array}\right.$
点评 本题主要考查函数奇偶性与单调性的综合应用,函数的周期性,利用函数奇偶性和周期性是解决本题的关键.

练习册系列答案
相关题目
19.已知向量$\overrightarrow{OP}$=(1,1),$\overrightarrow{{OP}_{1}}$=(4,-4),且P2点分有向线段$\overrightarrow{P{P}_{1}}$所成的比为-2,则$\overrightarrow{{OP}_{2}}$的坐标是( )
| A. | (-$\frac{5}{2}$,$\frac{3}{2}$) | B. | ($\frac{5}{2}$,-$\frac{3}{2}$) | C. | (7,-9) | D. | (9,-7) |
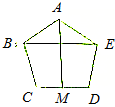 如图,正五边形ABCDE中,M为CD的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$,$\overrightarrow{DE}$=$\overrightarrow{d}$,试用$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AM}$和$\overrightarrow{BE}$.
如图,正五边形ABCDE中,M为CD的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$,$\overrightarrow{DE}$=$\overrightarrow{d}$,试用$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AM}$和$\overrightarrow{BE}$.