题目内容

18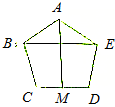．如图，正五边形ABCDE中，M为CD的中点，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，$\overrightarrow{CD}$=$\overrightarrow{c}$，$\overrightarrow{DE}$=$\overrightarrow{d}$，试用$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AM}$和$\overrightarrow{BE}$．

分析 利用向量的多边形法则即可得出．

解答 解：$\overrightarrow{AM}$=$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CM}$=$\overrightarrow{a}+\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$．
$\overrightarrow{BE}$=$\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}$=$\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}$．

点评 本题考查了向量的多边形法则，属于基础题．

练习册系列答案
相关题目
8．给出的四个命题：①存在实数φ，使函数f（x）=sin（x+φ）为偶函数；②“函数g（x）=$\frac{k-{2}^{x}}{1+k•{2}^{x}}$为奇函数”的充要条件是“k=1”；③对任意实数a，方程x2+ax-1=0有实数根；④数列{an}满足a1=1，an+1 =p•an+p（n∈N*），则“p=1”是“数列{an}是等差数列”的充要条件，其中真命题的序号是①③④．（写出所有真命题的序号）
9．解不等式：100（1+x）20＜120．
6．已知奇函数f（x）的定义域为（-∞，0）∪（0，+∞），若f（x）在（-∞，0）上为减函数，且f（-1）=0，则不等式f（x）＜0的解集为{x|-1＜x＜0或x＞1}．
13．在△ABC中，若BC=2，sinA=$\frac{2\sqrt{2}}{3}$，则$\overrightarrow{AB}$•$\overrightarrow{AC}$的最大值为（　　）
A．$\frac{1}{3}$B．$\frac{4}{5}$C．1D．3
3．已知函数f（x）满足f（x）•f（x+2）=13．
（1）求证：f（x）是周期函数；
（2）若f（1）=2，求f（99）的值．
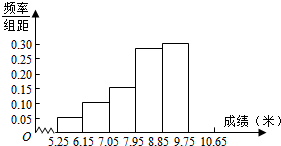10．某市为了解今年高中毕业生的体能状况，从本市某校高中毕业班中抽取一个班进行铅球测试，成绩在8.0米（精确到0.1米）以上的为合格．把所得数据进行整理后，分成6组画出频率分布直方图的一部分（如图），已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30，第6小组的频数是7．
（Ⅰ）求这次铅球测试成绩合格的人数；
（Ⅱ）用此次测试结果估计全市毕业生的情况．若从今年的高中毕业生中随机抽取两名，记X表示两人中成绩不合格的人数，求X的分布列及数学期望；
（Ⅲ）经过多次测试后，甲成绩在8～10米之间，乙成绩在9.5～10.5米之间，现甲、乙各投掷一次，求甲比乙投掷远的概率．
7．已知函数y=f（x）是定义在R上的偶函数，且对任意实数x，都有f（x+1）=f（x-1）成立，已知当x∈[1，2]时，f（x）=logax（a＞0且a≠1）．
（1）求x∈[-1，1]时，函数f（x）的表达式；
（2）求x∈[2k-1，2k+1]（k∈Z）时，函数f（x）的解析式．
8．将村庄甲、乙、丙看成三点，正好构成△ABC，角A、B、C的对边分别为a、b、c，tanC=3$\sqrt{7}$，若$\overrightarrow{CB}$•$\overrightarrow{CA}$=$\frac{5}{2}$，且甲到丙的距离与乙到丙的距离之和为9，则甲乙之间的距离为6．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网