题目内容
已知抛物线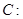
 上的点
上的点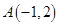 ,直线
,直线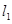 过点
过点 且与抛物线相切,直线
且与抛物线相切,直线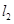 :
: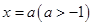 交抛物线于点
交抛物线于点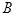 ,交直线
,交直线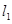 于点
于点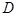 ,记
,记 的面积为
的面积为 ,抛物线和直线
,抛物线和直线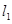 ,
,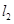 所围成的图形面积为
所围成的图形面积为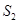 ,则
,则 ( )
( )
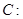
 上的点
上的点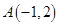 ,直线
,直线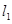 过点
过点 且与抛物线相切,直线
且与抛物线相切,直线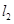 :
: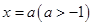 交抛物线于点
交抛物线于点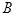 ,交直线
,交直线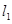 于点
于点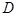 ,记
,记 的面积为
的面积为 ,抛物线和直线
,抛物线和直线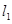 ,
,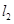 所围成的图形面积为
所围成的图形面积为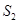 ,则
,则 ( )
( )A.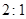 | B.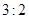 |
C.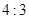 | D.随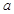 的值而变化 的值而变化 |
B
解:(1)由y=2x2,得y′=4x.当x=-1时,y'=-4.
∴l1的方程为y-2=-4(x+1),即y=-4x-2.(3分)
(2)由
y=2x2
x=a ,得:B点坐标为(a,2a2).由
x="a"
4x+y+12=0 ,得D点坐标(a,-4a-2).
∴点A到直线BD的距离为|a+1|.
|BD|=2a2+4a+2=2(a+1)2
∴S1=|a+1|3.
(3)当a>-1时,S1=(a+1)3,(8分)
S2=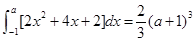
∴S1:S2="3" :2 .
当a<-1时,S1=-(a+1)3
S2=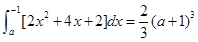
故S1:S2="3" :2,综上可得结论为B
∴l1的方程为y-2=-4(x+1),即y=-4x-2.(3分)
(2)由
y=2x2
x=a ,得:B点坐标为(a,2a2).由
x="a"
4x+y+12=0 ,得D点坐标(a,-4a-2).
∴点A到直线BD的距离为|a+1|.
|BD|=2a2+4a+2=2(a+1)2
∴S1=|a+1|3.
(3)当a>-1时,S1=(a+1)3,(8分)
S2=
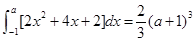
∴S1:S2="3" :2 .
当a<-1时,S1=-(a+1)3
S2=
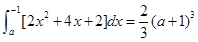
故S1:S2="3" :2,综上可得结论为B

练习册系列答案
相关题目
 过y轴上一点
过y轴上一点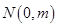 ,
,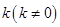 ,两端点
,两端点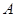 、
、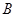 到y轴的距离之差为
到y轴的距离之差为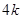 .
.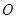 、
、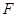 作动弦
作动弦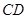 ,过
,过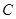 、
、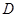 两点分别作抛物线的切线,设其交点为
两点分别作抛物线的切线,设其交点为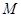 ,求点
,求点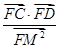 的值.
的值.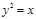 上的点到直线
上的点到直线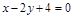 的距离最小的点的坐标是 .
的距离最小的点的坐标是 . 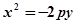 的焦点坐标为
的焦点坐标为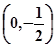 ,它与过点
,它与过点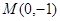 的直线
的直线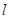 相交于A,B两点,O为坐标原点。
相交于A,B两点,O为坐标原点。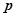 值;
值;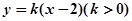 与抛物线
与抛物线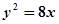 相交于
相交于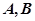 两点,
两点,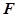 为抛物线的焦点,若
为抛物线的焦点,若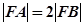 ,则
,则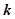 的值为 ______________.
的值为 ______________.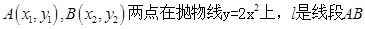 的垂直平分线.
的垂直平分线.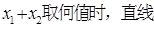
 ?
? 轴上截距的取值范围.
轴上截距的取值范围. 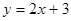 与抛物线
与抛物线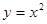 所围成的图形面积是
所围成的图形面积是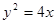 的焦点作一直线交抛物线于A(x1, y1)、B(x2, y2)两点,并且已知
的焦点作一直线交抛物线于A(x1, y1)、B(x2, y2)两点,并且已知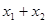 =6,那么
=6,那么 =( )
=( )