题目内容
如图,线段 过y轴上一点
过y轴上一点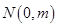 ,
, 所在直线的斜率为
所在直线的斜率为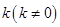 ,两端点
,两端点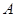 、
、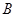 到y轴的距离之差为
到y轴的距离之差为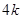 .
.
(Ⅰ)求出以y轴为对称轴,过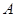 、
、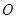 、
、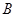 三点的抛物线方程;
三点的抛物线方程;
(Ⅱ)过抛物线的焦点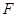 作动弦
作动弦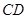 ,过
,过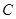 、
、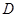 两点分别作抛物线的切线,设其交点为
两点分别作抛物线的切线,设其交点为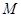 ,求点
,求点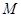 的轨迹方程,并求出
的轨迹方程,并求出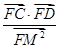 的值.
的值.
 过y轴上一点
过y轴上一点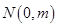 ,
, 所在直线的斜率为
所在直线的斜率为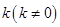 ,两端点
,两端点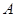 、
、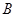 到y轴的距离之差为
到y轴的距离之差为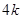 .
.(Ⅰ)求出以y轴为对称轴,过
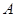 、
、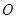 、
、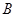 三点的抛物线方程;
三点的抛物线方程;(Ⅱ)过抛物线的焦点
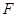 作动弦
作动弦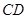 ,过
,过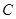 、
、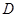 两点分别作抛物线的切线,设其交点为
两点分别作抛物线的切线,设其交点为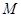 ,求点
,求点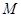 的轨迹方程,并求出
的轨迹方程,并求出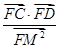 的值.
的值.(Ⅰ)抛物线方程为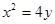 ; (Ⅱ)
; (Ⅱ)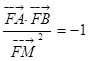 。
。
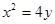 ; (Ⅱ)
; (Ⅱ)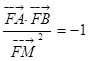 。
。(I)设 所在直线方程为
所在直线方程为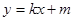 ,抛物线方程为
,抛物线方程为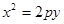
且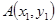 ,
, 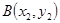 ,
,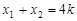 ,再让直线AB的方程与抛物线的方程联立,借助韦达定理建立关于p的方程,求出p值,确定出抛物线的方程.
,再让直线AB的方程与抛物线的方程联立,借助韦达定理建立关于p的方程,求出p值,确定出抛物线的方程.
(II) 设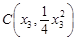 ,
,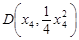 ,然后利用导数求出经过C、D的切线方程,求出交点M的坐标,设
,然后利用导数求出经过C、D的切线方程,求出交点M的坐标,设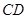 的直线方程为
的直线方程为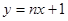 ,代入
,代入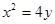 得
得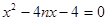 ,根据
,根据 是方程
是方程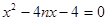 的两个根,确定点M的轨迹方程以后,解决此问题才有了正确的出口.
的两个根,确定点M的轨迹方程以后,解决此问题才有了正确的出口.
(Ⅰ)设 所在直线方程为
所在直线方程为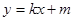 ,抛物线方程为
,抛物线方程为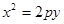 ,且
,且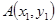 ,
, 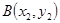 ,不妨设
,不妨设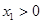 ,
,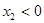
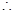
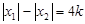 即
即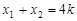
把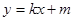 代入
代入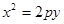 得
得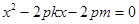
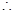
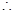
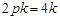
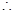
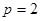 故所求抛物线方程为
故所求抛物线方程为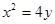 ---------4分
---------4分
(Ⅱ)设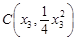 ,
,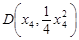
过抛物线上 、
、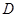 两点的切线方程分别是
两点的切线方程分别是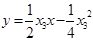 ,
,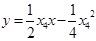
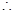 两条切线的交点
两条切线的交点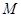 的坐标为
的坐标为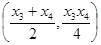
设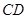 的直线方程为
的直线方程为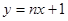 ,代入
,代入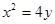 得
得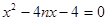
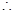
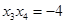 故
故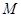 的坐标为
的坐标为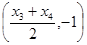 点
点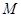 的轨迹为
的轨迹为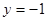 ---------------8分
---------------8分
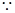
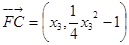
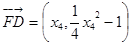
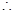
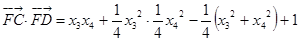
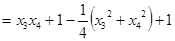
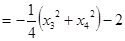
而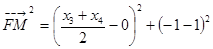
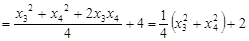
故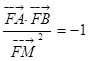 -----------------------------------12分
-----------------------------------12分
 所在直线方程为
所在直线方程为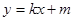 ,抛物线方程为
,抛物线方程为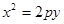
且
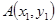 ,
, 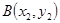 ,
,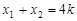 ,再让直线AB的方程与抛物线的方程联立,借助韦达定理建立关于p的方程,求出p值,确定出抛物线的方程.
,再让直线AB的方程与抛物线的方程联立,借助韦达定理建立关于p的方程,求出p值,确定出抛物线的方程.(II) 设
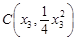 ,
,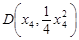 ,然后利用导数求出经过C、D的切线方程,求出交点M的坐标,设
,然后利用导数求出经过C、D的切线方程,求出交点M的坐标,设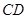 的直线方程为
的直线方程为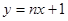 ,代入
,代入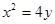 得
得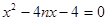 ,根据
,根据 是方程
是方程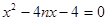 的两个根,确定点M的轨迹方程以后,解决此问题才有了正确的出口.
的两个根,确定点M的轨迹方程以后,解决此问题才有了正确的出口.(Ⅰ)设
 所在直线方程为
所在直线方程为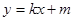 ,抛物线方程为
,抛物线方程为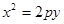 ,且
,且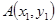 ,
, 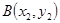 ,不妨设
,不妨设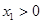 ,
,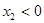
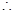
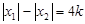 即
即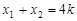
把
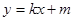 代入
代入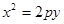 得
得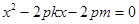
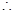
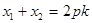
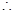
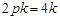
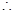
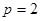 故所求抛物线方程为
故所求抛物线方程为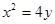 ---------4分
---------4分(Ⅱ)设
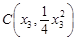 ,
,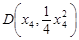
过抛物线上
 、
、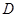 两点的切线方程分别是
两点的切线方程分别是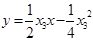 ,
,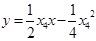
 两条切线的交点
两条切线的交点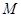 的坐标为
的坐标为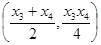
设
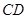 的直线方程为
的直线方程为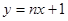 ,代入
,代入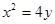 得
得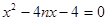
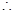
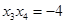 故
故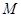 的坐标为
的坐标为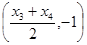 点
点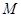 的轨迹为
的轨迹为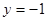 ---------------8分
---------------8分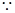
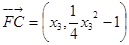
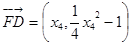
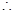
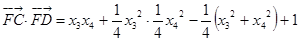
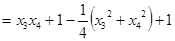
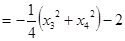
而
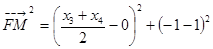
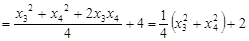
故
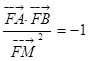 -----------------------------------12分
-----------------------------------12分
练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
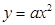 的准线方程是y=1,则此抛物线的标准方程为
的准线方程是y=1,则此抛物线的标准方程为 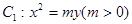 的准线与
的准线与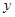 轴交于
轴交于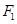 ,焦点为
,焦点为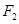 ,若椭圆
,若椭圆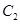 以
以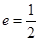 。
。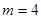 时求椭圆
时求椭圆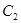 的方程;
的方程;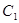 与直线
与直线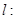
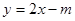 及
及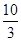 ,求抛物线
,求抛物线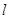 的方程
的方程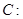
 上的点
上的点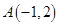 ,直线
,直线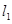 过点
过点 且与抛物线相切,直线
且与抛物线相切,直线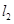 :
: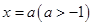 交抛物线于点
交抛物线于点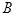 ,交直线
,交直线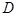 ,记
,记 的面积为
的面积为 ,抛物线和直线
,抛物线和直线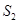 ,则
,则 ( )
( )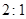
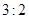
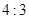
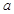 的值而变化
的值而变化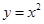 的焦点坐标是
的焦点坐标是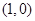
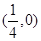
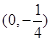
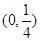
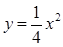 的焦点坐标是( )
的焦点坐标是( )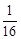 )
)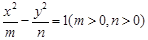 的离心率为2,有一个焦点与抛物线
的离心率为2,有一个焦点与抛物线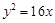 的焦点重合,则
的焦点重合,则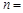 __________.
__________.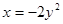 的准线方程是
的准线方程是 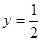
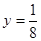
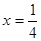
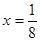
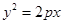 的焦点与双曲线
的焦点与双曲线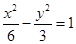 的右焦点重合,则
的右焦点重合,则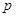 的值为
的值为