题目内容
求函数f（x）=x5+5x4+5x3+1在区间[-1，4]上的最大值与最小值．
f′（x）=5x4+20x3+15x2=5x2（x+3）（x+1），
当f′（x）=0得x=0，或x=-1，或x=-3，
∵0∈[-1，4]，-1∈[-1，4]，-3∉[-1，4]
列表：
又f（0）=0，f（-1）=0；右端点处f（4）=2625；
∴函数y=x5+5x4+5x3+1在区间[-1，4]上的最大值为2625，最小值为0．
当f′（x）=0得x=0，或x=-1，或x=-3，
∵0∈[-1，4]，-1∈[-1，4]，-3∉[-1，4]
列表：
又f（0）=0，f（-1）=0；右端点处f（4）=2625；
∴函数y=x5+5x4+5x3+1在区间[-1，4]上的最大值为2625，最小值为0．
练习册系列答案
相关题目
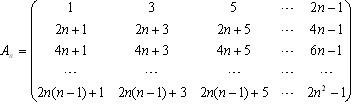任取An中的一个元素，记为x1；划去x1所在的行和列，将剩下的元素按原来的位置关系组成n-1阶方阵An-1，任取An-1中的一个元素，记为x2；划去x2所在的行和列，…；将最后剩下的一个元素记为xn，记Sn=x1+x2+…+xn，则