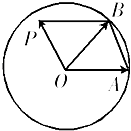题目内容
【题目】已知A(﹣1,0),B(1,0), ![]() =
= ![]() +
+ ![]() ,|
,| ![]() |+|
|+| ![]() |=4
|=4
(1)求P的轨迹E
(2)过轨迹E上任意一点P作圆O:x2+y2=3的切线l1 , l2 , 设直线OP,l1 , l2的斜率分别是k0 , k1 , k2 , 试问在三个斜率都存在且不为0的条件下, ![]() (
( ![]() +
+ ![]() )是否是定值,请说明理由,并加以证明.
)是否是定值,请说明理由,并加以证明.
【答案】
(1)解:如图因为 ![]() =
= ![]() +
+ ![]() ,所以四边形ACPB是平行四边形,
,所以四边形ACPB是平行四边形,
所以| ![]() |=|
|=| ![]() |,
|,
由| ![]() |+|
|+| ![]() |=4,得,|
|=4,得,| ![]() |+|
|+| ![]() |=4,
|=4,
所以P的轨迹是以A,B为焦点的椭圆,a=2,c=1,b= ![]() ,
,
所以方程为 ![]() =1
=1
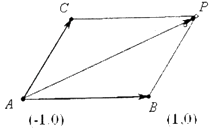
(2)解:设P(x0,y0),过P的斜率为k的直线为y﹣y0=k(x﹣x0),
由直线与圆O相切可得 ![]() =
= ![]() ,即:
,即: ![]() ,
,
由已知可知k1,k2是方程 ![]() 的两个根,
的两个根,
所以由韦达定理:k1+k2= ![]() ,k1k2=
,k1k2= ![]() ,
,
两式相除: ![]() +
+ ![]() =
= ![]() ,
,
又因为 ![]() =﹣
=﹣ ![]() ,
,
代入上式可得, ![]() (
( ![]() +
+ ![]() )=﹣
)=﹣ ![]() 为一个定值
为一个定值
【解析】(1)利用| ![]() |=|
|=| ![]() |,由|
|,由| ![]() |+|
|+| ![]() |=4,得,|
|=4,得,| ![]() |+|
|+| ![]() |=4,即可求P的轨迹E;(2)所以由韦达定理:k1+k2=
|=4,即可求P的轨迹E;(2)所以由韦达定理:k1+k2= ![]() ,k1k2=
,k1k2= ![]() ,两式相除:
,两式相除: ![]() +
+ ![]() =
= ![]() ,即可得出结论.
,即可得出结论.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目