题目内容
18．在平行四边形ABCD中，若$\overrightarrow{AB}$=（1，2），$\overrightarrow{AD}$=（2，3），则该平行四边形的面积为1．分析 由向量的数量积的定义和坐标表示，可得cosA，由同角的平方关系可得sinA，再由平行四边形的面积为S=|$\overrightarrow{AB}$|•|$\overrightarrow{AD}$|•sinA，计算即可得到所求．
解答 解：$\overrightarrow{AB}$•$\overrightarrow{AD}$=1×2+2×3=8，
又$\overrightarrow{AB}$•$\overrightarrow{AD}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AD}$|•cosA=$\sqrt{5}$•$\sqrt{13}$•cosA，
即有cosA=$\frac{8}{\sqrt{65}}$，
sinA=$\frac{1}{\sqrt{65}}$，
则该平行四边形的面积为S=|$\overrightarrow{AB}$|•|$\overrightarrow{AD}$|•sinA
=$\sqrt{5}$•$\sqrt{13}$•$\frac{1}{\sqrt{65}}$=1．
故答案为：1．
点评 本题考查向量的数量积的定义和坐标表示，考查平行四边形的面积，属于基础题．
练习册系列答案
相关题目
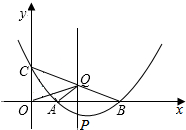已知如图，抛物线y=ax2+bx+2与x轴的交点是A（3，0）、B（6，0），与y轴的交点是C．