题目内容
9.已知等差数列{an}的前n项和为Sn,且a3=S3=3.(1)求{an}的通项公式;
(2)若{bn-an}是首项为1,公比为2的等比数列,求数列{bn}的前n项和.
分析 (1)由已知条件利用等差数列的通项公式和前n项和公式列出方程组,求出首项和公差,由此能求出等差数列{an}的{an}的通项公式.
(2)由{bn-an}是首项为1,公比为2的等比数列,求出bn=2n-1+2n+3,由此利用分组和法能求出数列{bn}的前n项和.
解答 解:(1)∵等差数列{an}的前n项和为Sn,且a3=S3=3,
∴$\left\{\begin{array}{l}{{a}_{1}+2d=3}\\{3{a}_{1}+\frac{3(3-1)}{2}d=3}\end{array}\right.$,
解得a1=-1,d=2,
∴an=-1+(n-1)×2=2n-3.
(2)∵{bn-an}是首项为1,公比为2的等比数列,
∴bn-an=bn-2n+3=2n-1,
∴bn=2n-1+2n+3,
∴数列{bn}的前n项和:
Sn=(1+2+22+…+2n-1)+2(1+2+3+…+n)+3×n
=$\frac{1-{2}^{n}}{1-2}$+2×$\frac{1+n}{2}$+3n
=2n+4n.
点评 本题考查数列的通项公式和前n项和公式的求法,是中档题,解题时要认真审题,注意等差数列的性质和分组求和法的合理运用.

练习册系列答案
相关题目
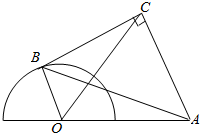 为改善居民的生活环境,政府拟将一公园进行改造扩建,已知原公园是直径为200米的半圆形,出入口在圆心O处,A为居民小区,OA的距离为200米,按照设计要求,以居民小区A和圆弧上点B为线段向半圆外作等腰直角三角形ABC(C为直角顶点),使改造后的公园成四边形OACB,如图所示.
为改善居民的生活环境,政府拟将一公园进行改造扩建,已知原公园是直径为200米的半圆形,出入口在圆心O处,A为居民小区,OA的距离为200米,按照设计要求,以居民小区A和圆弧上点B为线段向半圆外作等腰直角三角形ABC(C为直角顶点),使改造后的公园成四边形OACB,如图所示.