题目内容
对于定义域为A的函数f(x),如果任意的x1,x2∈A,当x1<x2时,都有f(x1)<f(x2),则称函数f(x)是A上的严格增函数;函数f(k)是定义在N*上,函数值也在N*中的严格增函数,并且满足条件f(f(k))=3k.
(1)证明:f(3k)=3f(k);
(2)求f(3k-1)(k∈N*)的值;
(3)是否存在p个连续的自然数,使得它们的函数值依次也是连续的自然数;若存在,找出所有的p值,若不存在,请说明理由.
(1)证明:f(3k)=3f(k);
(2)求f(3k-1)(k∈N*)的值;
(3)是否存在p个连续的自然数,使得它们的函数值依次也是连续的自然数;若存在,找出所有的p值,若不存在,请说明理由.
(1)见解析(2)2×3k-1(k∈N*)(3)存在p=3k-1+1
(1)证明:对k∈N*,f(f(k))=3k,∴f[f(f(k))]=f(3k)①
由已知f(f(k))=3k,∴f[f(f(k))]=3f(k),②
由①、②∴f(3k)=3f(k)
(2)若f(1)=1,由已知f(f(k))=3k得f(1)=3,矛盾;
设f(1)=a>1,∴f(f(1))=f(a)=3,③
由f(k)严格递增,即1<a⇒f(1)<f(a)=3,
∴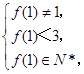 ∴f(1)=2,
∴f(1)=2,
由③f(f(1))=f(a)=3,故f(f(1))=f(2)=3.
∴f(1)=2,f(2)=3.
f(3)=3f(1)=6,f(6)=f(3·2)=3f(2)=9,
f(9)=3f(3)=18,f(18)=3f(6)=27,
f(27)=3f(9)=54,f(54)=3f(18)=81.
依此类推归纳猜出:f(3k-1)=2×3k-1(k∈N*).
下面用数学归纳法证明:
(1)当k=1时,显然成立;
(2)假设当k=l(l≥1)时成立,即f(3l-1)=2×3l-1,
那么当k=l+1时,f(3l)=f(3×3l-1)=3f(3l-1)=3×2×3l-1=2·3l.猜想成立,由(1)、(2)所证可知,对k∈N*f(3k-1)=2×3k-1成立.
(3)存在p=3k-1+1,当p个连续自然数从3k-1→2×3k-1时,函数值正好也是p个连续自然数从f(3k-1)=2×3k-1→f(2×3k-1)=3k.
由已知f(f(k))=3k,∴f[f(f(k))]=3f(k),②
由①、②∴f(3k)=3f(k)
(2)若f(1)=1,由已知f(f(k))=3k得f(1)=3,矛盾;
设f(1)=a>1,∴f(f(1))=f(a)=3,③
由f(k)严格递增,即1<a⇒f(1)<f(a)=3,
∴
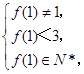 ∴f(1)=2,
∴f(1)=2, 由③f(f(1))=f(a)=3,故f(f(1))=f(2)=3.
∴f(1)=2,f(2)=3.
f(3)=3f(1)=6,f(6)=f(3·2)=3f(2)=9,
f(9)=3f(3)=18,f(18)=3f(6)=27,
f(27)=3f(9)=54,f(54)=3f(18)=81.
依此类推归纳猜出:f(3k-1)=2×3k-1(k∈N*).
下面用数学归纳法证明:
(1)当k=1时,显然成立;
(2)假设当k=l(l≥1)时成立,即f(3l-1)=2×3l-1,
那么当k=l+1时,f(3l)=f(3×3l-1)=3f(3l-1)=3×2×3l-1=2·3l.猜想成立,由(1)、(2)所证可知,对k∈N*f(3k-1)=2×3k-1成立.
(3)存在p=3k-1+1,当p个连续自然数从3k-1→2×3k-1时,函数值正好也是p个连续自然数从f(3k-1)=2×3k-1→f(2×3k-1)=3k.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 )内各有一个零点,求实数a的范围.
)内各有一个零点,求实数a的范围.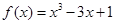 在区间
在区间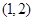 上的零点的近似值(精确度
上的零点的近似值(精确度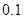 )是 .
)是 . 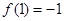





 ,若
,若 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )


