题目内容
(本小题满分14分)已知函数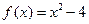 ,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n ÎN *),x1=4.
,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n ÎN *),x1=4.
(Ⅰ)用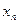 表示xn+1;
表示xn+1;
(Ⅱ)记an=lg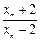 ,证明数列{an}成等比数列,并求数列{xn}的通项公式;
,证明数列{an}成等比数列,并求数列{xn}的通项公式;
(Ⅲ)若bn=xn-2,试比较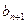 与
与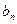 的大小.
的大小.
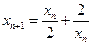 ,
, ,
,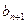 <
<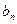
解析解:(Ⅰ)由题可得 ................2分
................2分
所以曲线 在点
在点 处的切线方程是:
处的切线方程是: .
.
即 . ...............4分
. ...............4分
令 ,得
,得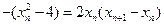 ,即
,即 .
.
显然 ,∴
,∴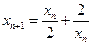 . ..................6分
. ..................6分
(Ⅱ)由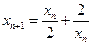 ,知
,知 ,同理
,同理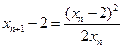 .
.
故 .
.
从而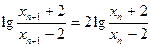 ,即
,即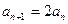 .所以,数列
.所以,数列 成等比数列. ...8分
成等比数列. ...8分
故 ,即
,即 ,从而
,从而 ,
,
所以 . ..................10分
. ..................10分
(Ⅲ)由(Ⅱ)知 ,
,
∴ ; ...........12分
; ...........12分
∴ ,
,
故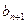 <
<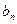 . ............14分
. ............14分
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u

 导学全程练创优训练系列答案
导学全程练创优训练系列答案 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)