题目内容
3.设函数f(x)=$\frac{x+2}{x+1}$,指出f(x)的单调区间,并证明f(x)在其单调区间上的单调性.分析 分离常数,将原函数变成f(x)=1+$\frac{1}{x+1}$,根据反比例函数的单调性即知f(x)在(-∞,-1),(-1,+∞)上单调递减,用定义证明:在定义域内任意设x1<x2,然后作差,通分即可判断x1,x2∈(-∞,-1),和x1,x2∈(-1,+∞)时的f(x1)与f(x2)的大小关系,从而证明出函数f(x)的单调性.
解答 解:f(x)=$\frac{x+2}{x+1}=1+\frac{1}{x+1}$;
∴f(x)在(-∞,-1),(-1,+∞)上单调递减,用定义证明如下:
设x1<x2,则:f(x1)-f(x2)=$\frac{1}{{x}_{1}+1}-\frac{1}{{x}_{2}+1}=\frac{{x}_{2}-{x}_{1}}{({x}_{1}+1)({x}_{2}+1)}$;
∴x1<x2<-1,或-1<x1<x2时,x2-x1>0,(x1+1)(x2+1)>0;
∴$\frac{{x}_{2}-{x}_{1}}{({x}_{1}+1)({x}_{2}+1)}>0$;
即f(x1)>f(x2);
∴f(x)在(-∞,-1),(-1,+∞)上单调递减.
点评 考查反比例函数的单调性,分离常数法的运用,减函数的定义,以及根据减函数的定义证明一个函数为减函数的方法和过程,作差的方法比较f(x1)与f(x2),作差后是分式的一般通分.

练习册系列答案
相关题目
18.一个几何体的三视图如图所示,则该几何体的体积为( )
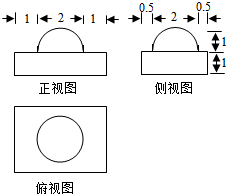

| A. | 12+$\frac{π}{3}$ | B. | 12+$\frac{2π}{3}$ | C. | 12+π | D. | 12+$\frac{4π}{3}$ |
15.已知x、y∈(-$\sqrt{2}$,$\sqrt{2}$),且x•y=1,则$\frac{2}{2-{x}^{2}}$+$\frac{4}{4-{y}^{2}}$的最小值为( )
| A. | $\frac{20}{7}$ | B. | $\frac{12}{7}$ | C. | $\frac{16+4\sqrt{2}}{7}$ | D. | $\frac{16-4\sqrt{2}}{7}$ |
12.已知等差数列{an}满足a2=3,a5=9,若数列{bn}满足b1=3,bn+1=abn,则{bn}的通项公式为bn=( )
| A. | 2n-1 | B. | 2n+1 | C. | 2n+1-1 | D. | 2n-1+2 |
13.下列四个命题中真命题的是( )
| A. | 经过定点p(x0,y0)的直线都可能用方程y-y0=k(x-x0)表示 | |
| B. | 经过任意两个不同的点p1(x1,y1),p2(x2,y2)的直线都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)表示 | |
| C. | 经过定点A(0,b)的直线都可以用方程y=kx+b表示 | |
| D. | 不经过原点的直线都可以用方程$\frac{x}{a}$+$\frac{y}{b}$=1表示 |
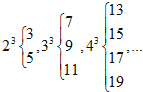 仿此,若m3的“分裂”数中有一个是73,则m的值为9.
仿此,若m3的“分裂”数中有一个是73,则m的值为9.