题目内容
设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(1)若l在两坐标轴上截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
(1)若l在两坐标轴上截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
(1)3x+y=0或x+y+2=0
(2)(-∞,-1]
(2)(-∞,-1]
解:(1)当直线过原点时,该直线在x轴和y轴上的截距为零,∴a=2,方程即为3x+y=0.
当直线不经过原点时,截距存在且均不为0,
∴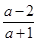 =a-2,即a+1=1.
=a-2,即a+1=1.
∴a=0,方程即为x+y+2=0.综上,l的方程为3x+y=0或x+y+2=0.
(2)将l的方程化为y=-(a+1)x+a-2,
∴ 或
或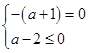
∴a≤-1.
综上可知a的取值范围是(-∞,-1].
当直线不经过原点时,截距存在且均不为0,
∴
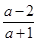 =a-2,即a+1=1.
=a-2,即a+1=1.∴a=0,方程即为x+y+2=0.综上,l的方程为3x+y=0或x+y+2=0.
(2)将l的方程化为y=-(a+1)x+a-2,
∴
 或
或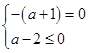
∴a≤-1.
综上可知a的取值范围是(-∞,-1].

练习册系列答案
相关题目
 与直线
与直线 的交点位于第一象限,则实数a的取值范围是( )
的交点位于第一象限,则实数a的取值范围是( )


 或
或




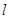 经过点
经过点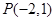 .
.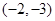 ,求直线
,求直线 ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.


