题目内容
(2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率 ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.

(1)求该椭圆的标准方程;
(2)取垂直于x轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若PQ⊥P'Q,求圆Q的标准方程.

 ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,|AA′|=4.
(1)求该椭圆的标准方程;
(2)取垂直于x轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若PQ⊥P'Q,求圆Q的标准方程.

(1)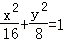 (2)
(2)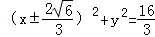
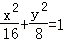 (2)
(2)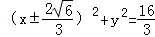
(1)由题意知点A(﹣c,2)在椭圆上,则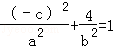 ,即
,即 ①
①
∵离心率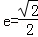 ,∴
,∴ ②
②
联立①②得: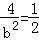 ,所以b2=8.
,所以b2=8.
把b2=8代入②得,a2=16.
∴椭圆的标准方程为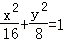 ;
;
(2)设Q(t,0),圆Q的半径为r,则圆Q的方程为(x﹣t)2+y2=r2,
不妨取P为第一象限的点,因为PQ⊥P'Q,则P(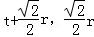 )(t>0).
)(t>0).
联立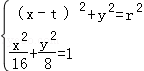 ,得x2﹣4tx+2t2+16﹣2r2=0.
,得x2﹣4tx+2t2+16﹣2r2=0.
由△=(﹣4t)2﹣4(2t2+16﹣2r2)=0,得t2+r2=8
又P(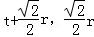 )在椭圆上,所以
)在椭圆上,所以 .
.
整理得,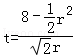 .
.
代入t2+r2=8,得 .
.
解得: .所以
.所以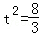 ,
,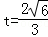 .
.
此时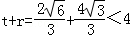 .
.
满足椭圆上的其余点均在圆Q外.
由对称性可知,当t<0时,t=﹣ ,
, .
.
故所求椭圆方程为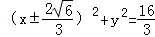 .
.
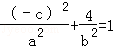 ,即
,即 ①
①∵离心率
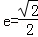 ,∴
,∴ ②
②联立①②得:
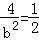 ,所以b2=8.
,所以b2=8.把b2=8代入②得,a2=16.
∴椭圆的标准方程为
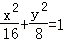 ;
;(2)设Q(t,0),圆Q的半径为r,则圆Q的方程为(x﹣t)2+y2=r2,
不妨取P为第一象限的点,因为PQ⊥P'Q,则P(
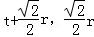 )(t>0).
)(t>0).联立
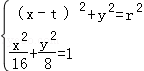 ,得x2﹣4tx+2t2+16﹣2r2=0.
,得x2﹣4tx+2t2+16﹣2r2=0.由△=(﹣4t)2﹣4(2t2+16﹣2r2)=0,得t2+r2=8
又P(
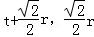 )在椭圆上,所以
)在椭圆上,所以 .
.整理得,
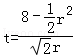 .
.代入t2+r2=8,得
 .
.解得:
 .所以
.所以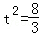 ,
,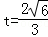 .
.此时
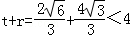 .
.满足椭圆上的其余点均在圆Q外.
由对称性可知,当t<0时,t=﹣
 ,
, .
.故所求椭圆方程为
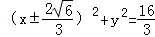 .
.
练习册系列答案
相关题目
 在
在 轴上的截距为 .
轴上的截距为 .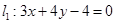 与
与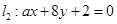 之间的距离是 .
之间的距离是 .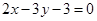 和
和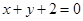 的交点且与直线
的交点且与直线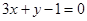 垂直的直线方程.
垂直的直线方程.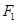 ,
,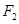 是双曲线
是双曲线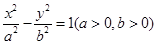 的左,右焦点,若双曲线左支上存在一点
的左,右焦点,若双曲线左支上存在一点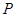 与点
与点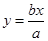 对称,则该双曲线的离心率为 ( )
对称,则该双曲线的离心率为 ( )



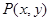 满足到定点
满足到定点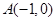 的距离与到定点
的距离与到定点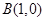 距离之比为
距离之比为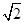 .
.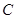 的方程;
的方程;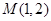 的直线
的直线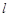 与曲线
与曲线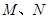 ,若
,若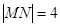 ,求直线
,求直线