题目内容
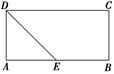
AB为圆O的直径,点E、F在圆上,AB//EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1。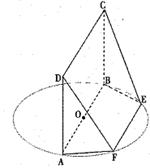
(I)求证:BF⊥平面DAF;
(II)求ABCD与平面CDEF所成锐二面角的某三角函数值;
(III)求多面体ABCDFE的体积。
(I)先证AD⊥平面ABEF,∴AD⊥BF;
由AB为圆O的直径,得AF⊥BF,且AF∩AD=A,可得BF⊥平面DAF;
(II)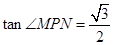 ;
;
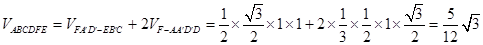
解析试题分析:(I)证明:因为平面ABCD⊥平面ABEF,AD⊥AB,
∴AD⊥平面ABEF,∴AD⊥BF;
又∵AB为圆O的直径,∴AF⊥BF,
AF∩AD=A,
∴BF⊥平面DAF; 4分
(II)取AB,CD,EF的中点M,P,N(如图所示)
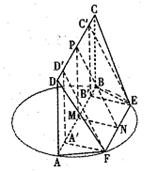
易证∠MPN为所求二面角的平面角。
根据题意
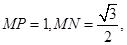
故
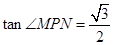 9分
9分(III)作
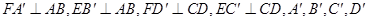 为垂足,则
为垂足,则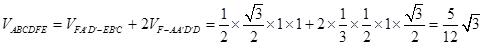
12分
考点:本题主要考查立体几何中的垂直关系、角及体积计算。
点评:中档题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用空间向量,省去繁琐的证明,也是解决立体几何问题的一个基本思路。对计算能力要求较高。本题中体积计算利用了整体与局部的关系。

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
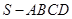 的底面
的底面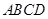 是直角梯形,
是直角梯形,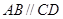 ,
,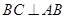 ,侧面
,侧面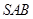 为正三角形,
为正三角形,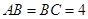 ,
,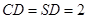 .如图所示.
.如图所示.
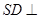 平面
平面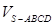 .
.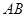 是半圆
是半圆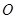 的直径,
的直径, 是半圆
是半圆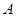 、
、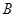 外的一个动点,
外的一个动点,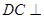 平面
平面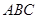 ,
,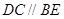 ,
,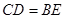 ,
,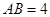 ,
,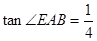 .
.
 平面
平面 ;
;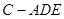 的体积取得最大值,请说明理由并求出这个最大值.
的体积取得最大值,请说明理由并求出这个最大值. 的底面是正方形,
的底面是正方形, ,点
,点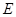 在棱
在棱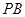 上.
上.
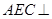 平面
平面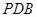 ;
;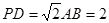 ,且
,且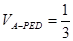 时,确定点
时,确定点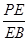 的值.
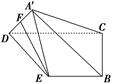
的值. 是正三角形,AB
是正三角形,AB 平面BCD,
平面BCD, ,E为BC的中点,F在棱AC上,且
,E为BC的中点,F在棱AC上,且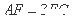


 .
.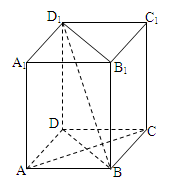
 棱长为1,
棱长为1, 是
是 的中点,
的中点, 是
是 的中点.
的中点. 
 ;
; 的余弦值.
的余弦值.