题目内容
如图:在三棱锥D-ABC中,已知 是正三角形,AB
是正三角形,AB 平面BCD,
平面BCD, ,E为BC的中点,F在棱AC上,且
,E为BC的中点,F在棱AC上,且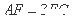

(1)求三棱锥D-ABC的表面积;
(2)求证AC⊥平面DEF;
(3)若M为BD的中点,问AC上是否存在一点N,使MN∥平面DEF?若存在,说明点N的位置;若不存在,试说明理由.
(1)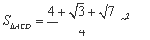
(2)先证EF⊥AC,再证DE⊥AC,即可证AC⊥平面DEF
(3)存在这样的点N,当CN=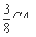 时,MN∥平面DEF.
时,MN∥平面DEF.
解析试题分析:
解:(1)∵AB⊥平面BCD,∴AB⊥BC,AB⊥BD.∵△BCD是正三角形,且AB=BC=a,∴AD=AC=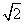 a.设G为CD的中点,则CG=
a.设G为CD的中点,则CG=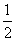 a,AG=
a,AG=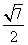 a.∴S△ABC=S△ABD=
a.∴S△ABC=S△ABD=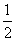 a2,S△BCD=
a2,S△BCD=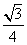 a2,S△ACD=
a2,S△ACD=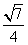 a2.三棱锥D-ABC的表面积为S△ACD=
a2.三棱锥D-ABC的表面积为S△ACD=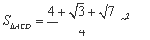
(2)取AC的中点H,∵AB=BC,∴BH⊥AC.∵AF=3FC,∴F为CH的中点.∵E为BC的中点,∴EF∥BH.则EF⊥AC.∵△BCD是正三角形,∴DE⊥BC.∵AB⊥平面BCD,∴AB⊥DE.∵AB∩BC=B,∴DE⊥平面ABC.∴DE⊥AC.∵DE∩EF=E,∴AC⊥平面DEF.
(3)存在这样的点N,当CN=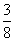 CA时,MN∥平面DEF.连CM,设CM∩DE=O,连OF.由条件知,O为△BCD的重心,CO=
CA时,MN∥平面DEF.连CM,设CM∩DE=O,连OF.由条件知,O为△BCD的重心,CO=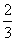 CM.∴当CF=
CM.∴当CF=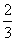 CN时,MN∥OF.∴CN=
CN时,MN∥OF.∴CN=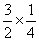 •CA=
•CA=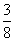 CA.
CA.
考点:棱锥的结构特征
点评:本题考查棱锥的结构特征,证明线面垂直,线面平行,考查逻辑思维能力,是中档题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
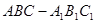 的三视图如图所示,
的三视图如图所示,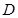 是
是 的中点.
的中点.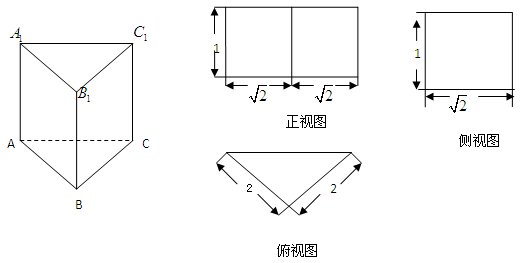
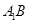 ∥平面
∥平面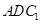 ;
;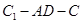 的余弦值;
的余弦值;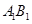 上是否存在点
上是否存在点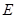 ,使
,使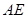 与
与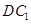 成
成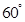 角?若存在,确定
角?若存在,确定 平面ABCD,
平面ABCD, ,E是PC上的一点.
,E是PC上的一点.
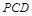 ;
;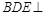 平面
平面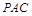 ;
; 为多长时,
为多长时, 平面
平面 ?
? 中,
中,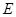 是
是 的中点.
的中点.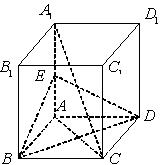
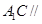 平面
平面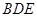 ;
;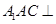 平面
平面 ,E、F分别为线段PD和BC的中点.
,E、F分别为线段PD和BC的中点.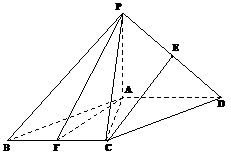
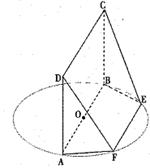
 为圆
为圆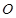 的直径,点
的直径,点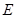 、
、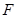 在圆
在圆 所在的平面和圆
所在的平面和圆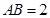 ,
, .
.
 平面
平面 ;
; 的体积.
的体积.
 ABC=60。,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
ABC=60。,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.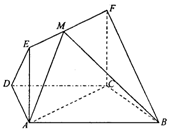
 ,求
,求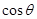 .
.