题目内容
如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,且AB=1,D1D=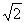 .
.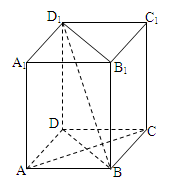
(1)求直线D1B与平面ABCD所成角的大小;
(2)求证:AC⊥平面BB1D1D.
(1)45º;(2)利用线线垂直证明线面垂直
解析试题分析:(1)因为D1D⊥面ABCD,所以BD为直线B D1在平面ABCD内的射影,
所以∠D1BD为直线D1B与平面ABCD所成的角, 2分
又因为AB=1,所以BD=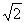 ,在Rt△D1DB中,
,在Rt△D1DB中,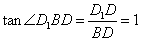 ,
,
所以∠D1BD=45º,所以直线D1B与平面ABCD所成的角为45º; 4分
(2)明:因为D1D⊥面ABCD,AC在平面ABCD内,所以D1D⊥AC,
又底面ABCD为正方形,所以AC⊥BD, 6分
因为BD与D1D是平面BB1D1D内的两条相交直线,
所以AC⊥平面BB1D1D. 8分
考点:本题考查了空间中的线面关系
点评:此类问题常考查空间中平行关系与垂直关系的证明以及空间角、几何体体积的计算,这是立体几何的重点内容.证明的关键是熟练掌握并灵活运用相关的判定定理与性质定理

练习册系列答案
相关题目
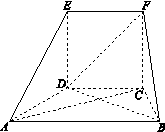
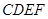 为正方形,面
为正方形,面 为等腰梯形,
为等腰梯形, ,
, ,
,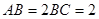 ,
,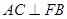 .
.
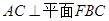 ;
;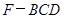 的体积;
的体积; 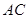 上是否存在点
上是否存在点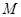 ,使
,使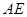 //平面
//平面 ?证明你的结论.
?证明你的结论. 中,
中, 是
是 的中点.
的中点.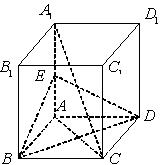
 平面
平面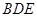 ;
; 平面
平面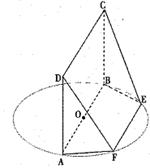
 为圆
为圆 的直径,点
的直径,点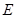 、
、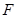 在圆
在圆 所在的平面和圆
所在的平面和圆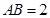 ,
, .
.
 平面
平面 ;
; 的体积.
的体积.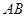 为圆
为圆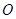 的直径,点
的直径,点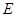 、
、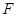 在圆
在圆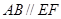 ,矩形
,矩形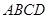 所在的平面与圆
所在的平面与圆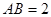 ,
,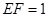 .
.
 平面
平面 ;
; 的长为何值时,平面
的长为何值时,平面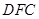 与平面
与平面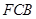 所成的锐二面角的大小为
所成的锐二面角的大小为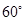 ?
?
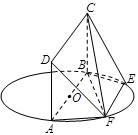
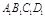 的底面
的底面 为菱 形 ,AC∩BD=O侧棱
为菱 形 ,AC∩BD=O侧棱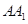 ⊥BD,点F为
⊥BD,点F为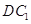 的中点.
的中点.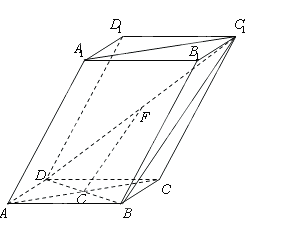
 平面
平面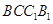 ;
;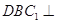 平面
平面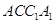 .
. 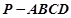 中,侧棱
中,侧棱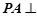 底面
底面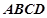 ,底面
,底面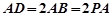 ,
,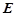 为
为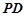 的上一点,且
的上一点,且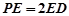 ,
, 为PC的中点.
为PC的中点.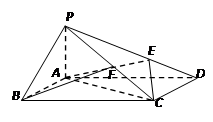

 平面AEC;
平面AEC;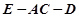 的余弦值.
的余弦值.