题目内容
5. 如图,四棱锥S-ABCD的底面是正方形,SA⊥平面ABCD,SA=$\sqrt{2}$AB,点E在棱SC上.
如图,四棱锥S-ABCD的底面是正方形,SA⊥平面ABCD,SA=$\sqrt{2}$AB,点E在棱SC上.(Ⅰ)若E为SC的中点,求证:SA∥平面BDE;
(Ⅱ)在(Ⅰ)的条件下,求CE与平面BDE所成的角.
分析 (Ⅰ)要证明SA∥平面BDE,只需证明SA平行于平面BDE内的一条直线即可,而E为中点,所以连接AC、BD交于点O.由条件知道O为AC中点,从而EO为三角形SAC的中位线,从而得到SA∥OE,得证;
(Ⅱ)证明∠CEO为CE与平面BDE所成的角,即可得出结论.
解答 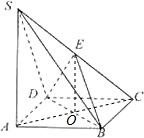 (Ⅰ)证明:设AC与BD的交点为O,连接OE,
(Ⅰ)证明:设AC与BD的交点为O,连接OE,
因为四边形ABCD是正方形,所以O为AC的中点,
又E为SC的中点,所以OE为三角形SAC的中位线,所以SA∥OE,
又OE?面BDE,SA?面BDE,
所以,SA∥平面BDE;
(Ⅱ)解:因为SA⊥平面ABCD,所以SA⊥OC,
因为SA∥EO,所以EO⊥OC,
因为四边形ABCD是正方形,所以BD⊥OC,
所以OC⊥平面BDE,
所以∠CEO为CE与平面BDE所成的角.
设正方形的边长为a,则EO=$\frac{1}{2}$SA=$\frac{\sqrt{2}}{2}$a,
Rt△COE中,tan∠CEO=$\frac{OC}{EO}$=1,所以∠CEO=45°,
所以CE与平面BDE所成的角为45°.
点评 本题考查线面平行的判定,直线与平面所成的觉,线面平行转化为线线平行是解题的关键.

练习册系列答案
相关题目
16.a=$\frac{1}{2}$cos6°-$\frac{\sqrt{3}}{2}$sin6°,b=2sin13°cos13°,c=$\sqrt{\frac{1-cos50°}{2}}$,则( )
| A. | a<c<b | B. | a<b<c | C. | a>b>c | D. | b<c<a |
13.已知“x>k”是“$\frac{2-x}{x+1}$<0”的充分不必要条件,则k的取值范围是( )
| A. | [2,+∞) | B. | [1,+∞) | C. | (-1,+∞) | D. | (-∞,-1] |
20.已知a<0,-1<b<0,则a,ab,ab2的大小关系式( )
| A. | a>ab>ab2 | B. | ab2>ab>a | C. | ab>a>ab2 | D. | ab>ab2>a |
10.等差数列{an}中,首项a1>0,公差d≠0,前n项和为Sn(n∈N*).有下列命题
①若S3=S11,则必有S14=0;
②若S3=S11,则必有S7是Sn中最大的项;
③若S7>S8,则必有S8>S9;
④若S7>S8,则必有S6>S9
其中正确的命题的个数是( )
①若S3=S11,则必有S14=0;
②若S3=S11,则必有S7是Sn中最大的项;
③若S7>S8,则必有S8>S9;
④若S7>S8,则必有S6>S9
其中正确的命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.正四棱锥(底面是正方形,顶点在底面的射影落在底面中心的四棱锥)P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,如果球O的表面积是4π,则四棱锥P-ABCD的体积为( )
| A. | $\frac{16}{3}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | $\frac{4}{3}$ |
14.观察两个变量(存在线性相关关系)得如下数据:
则两变量间的线性回归方程为( )
| x | -10 | -6.99 | -5.01 | -2.98 | 3.98 | 5 | 7.99 | 8.01 |
| y | -9 | -7 | -5 | -3 | 4.01 | 4.99 | 7 | 8 |
| A. | $\hat y$=$\frac{1}{2}$x+1 | B. | $\hat y$=x | C. | $\hat y$=2x+$\frac{1}{3}$ | D. | $\hat y$=x+1 |
15. 如图,两个直径分别为36cm和16cm的球,靠在一起放在同一水平面上,组成如图所示的几何体,则该几何体的俯视图的圆心距是( )
如图,两个直径分别为36cm和16cm的球,靠在一起放在同一水平面上,组成如图所示的几何体,则该几何体的俯视图的圆心距是( )
 如图,两个直径分别为36cm和16cm的球,靠在一起放在同一水平面上,组成如图所示的几何体,则该几何体的俯视图的圆心距是( )
如图,两个直径分别为36cm和16cm的球,靠在一起放在同一水平面上,组成如图所示的几何体,则该几何体的俯视图的圆心距是( )| A. | 10cm | B. | 24cm | C. | 26cm | D. | 52cm |