Question

【题目】数列的前项和为，，且，，成等差数列.

(1)求的值，并证明为等比数列；

(2)设，若对任意的，不等式恒成立，试求实数的取值范围.

Answer 1

【答案】(1) ：数列为等比数列证明见详解；(2)

【解析】

(1)带值计算可得，利用与的关系，可得与一个递推关系，利用配凑法，根据等比数列的定义，可得结果.

(2)根据(1)的结论，可得，进一步得到，然后代入，得到含参数关于的一元二次不等式，构造新函数，结合新函数的性质可得结果.

(1)因为 ，，成等差数列.

所以 ①，由 ②

当时，，即 ③

由①，③可知

当时

④

②-④：

即

又，所以

所以

所以数列是以为首项，

为公比的等比数列

(2)由(1)可知

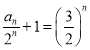，所以

所以

又

所以

化简可得

对任意的，

不等式恒成立

即恒成立

令

当时，则，恒成立，满足条件.

当时，开口向上，不恒成立，不符合

当时，

对称轴且开口向上

所以在递减

而

恒成立

综上所述：