题目内容
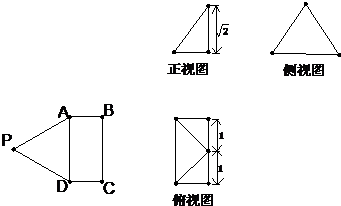
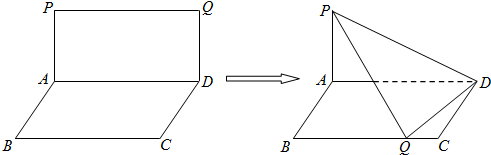
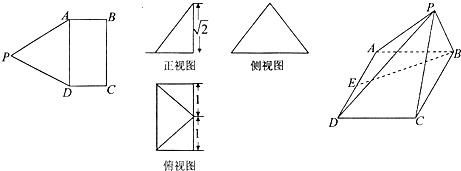
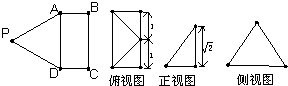
如图,矩形ABCD与ADQP所在平面垂直,将矩形ADQP沿PD对折,使得翻折后点Q落在BC上,设AB=1,PA=h,AD=y.
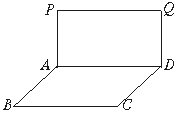
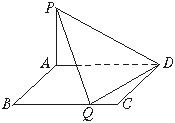
(1)试求y关于h的函数解析式;
(2)当y取最小值时,指出点Q的位置,并求出此时AD与平面PDQ所成的角;
(3)在条件(2)下,求三棱锥P—ADQ内切球的半径.
答案:
解析:
解析:
|
解:(1)显然h>1,连接AQ, ∵平面ABCD⊥平面ADQP,PA⊥AD, ∴PA⊥平面ABCD,由已知PQ⊥DQ, ∴AQ⊥DQ,AQ=y2-h2. ∵Rt△ABQ∽Rt△QCD,CQ= ∴ ∴y= (2)y= = 当且仅当 此时CQ=1,即Q为BC的中点,于是由DQ⊥平面PAQ,知平面PDQ⊥平面PAQ,PQ是其交线,则过A作AE⊥平面PDQ,∴∠ADE就是AD与平面PDQ所成的角,由已知得AQ= (3)设三棱锥P-ADQ的内切球半径为r, 则 ∵VP-ADQ= S△PAD= ∴r= |

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
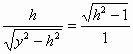 .
.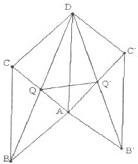 如图,矩形ABCD与矩形AB′C′D全等,且所在平面所成的二面角为a,记两个矩形对角线的交点分别为Q,Q′,AB=a,AD=b.
如图,矩形ABCD与矩形AB′C′D全等,且所在平面所成的二面角为a,记两个矩形对角线的交点分别为Q,Q′,AB=a,AD=b.