题目内容
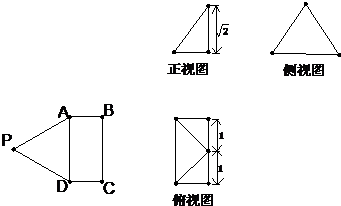
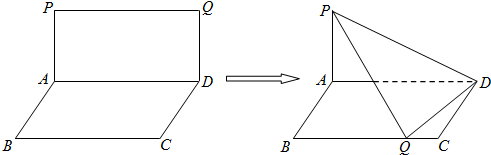
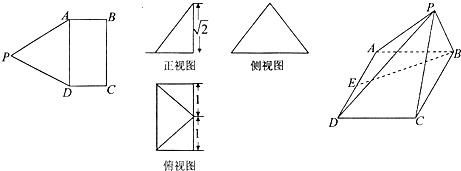
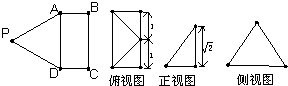
如图,矩形ABCD与正三角形APD中,AD=2,DC=1,E为AD的中点.现将正三角形APD沿AD折起,得到四棱锥的三视图如右图,则四棱锥P-ABCD的侧面积为
2
+
| 3 |
| 2 |
2
+
| 3 |
| 2 |

分析:先由三视图画出几何体的直观图,辨清其中的线面关系和数量关系,再利用三角形面积公式分别求四个面的面积相加即可
解答:解:由三视图可知四棱锥的直观图如图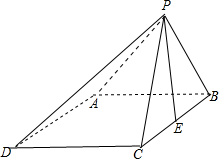 :其中PE⊥平面ABCD,CE=BE=1,PE=
:其中PE⊥平面ABCD,CE=BE=1,PE=
,AD=2,DC=1,PC=PB=
=
∴平面PBC⊥平面ABCD,从而DC⊥平面PBC,AB⊥平面PBC,
∴DC⊥PC,AB⊥PB
∴S△PBC=
×2×
=
S△PDC=S△PAB=
×1×
=
S△PAB=
×2×2×
=
∴四棱锥P-ABCD的侧面积为S△PBC+S△PDC+S△PAB+S△PAB=
+
+
+
=2
+
故答案为2
+
 :其中PE⊥平面ABCD,CE=BE=1,PE=
:其中PE⊥平面ABCD,CE=BE=1,PE=| 2 |
| 2+1 |
| 3 |
∴平面PBC⊥平面ABCD,从而DC⊥平面PBC,AB⊥平面PBC,
∴DC⊥PC,AB⊥PB
∴S△PBC=
| 1 |
| 2 |
| 2 |
| 2 |
S△PDC=S△PAB=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
S△PAB=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴四棱锥P-ABCD的侧面积为S△PBC+S△PDC+S△PAB+S△PAB=
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
故答案为2
| 3 |
| 2 |
点评:本题考查了几何体三视图的识别和应用,三视图与直观图间的关系,空间的线面垂直及平行关系,几何体侧面积的计算方法

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
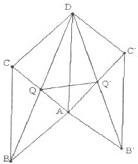 如图,矩形ABCD与矩形AB′C′D全等,且所在平面所成的二面角为a,记两个矩形对角线的交点分别为Q,Q′,AB=a,AD=b.
如图,矩形ABCD与矩形AB′C′D全等,且所在平面所成的二面角为a,记两个矩形对角线的交点分别为Q,Q′,AB=a,AD=b.