题目内容
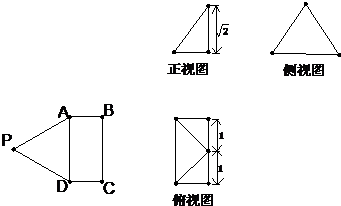
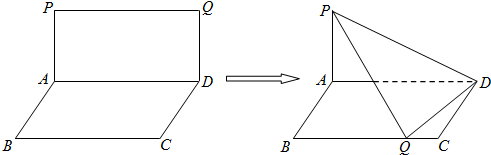
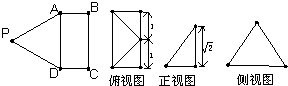
如图,矩形ABCD与正三角形APD中,AD=2,DC=1,E为AD的中点,现将正三角形APD沿AD折起,得到四棱锥P-ABCD,该四棱锥的三视图如下: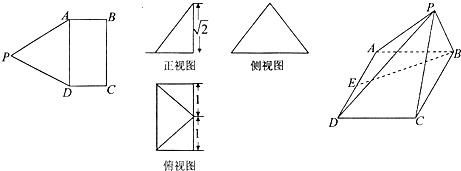
(I)求四棱锥P-ABCD的体积;
(Ⅱ)求异面直线BE,PD所成角的大小;
(Ⅲ)求二面角A-PD-C的正弦值.
分析:(I)由已知中的三视图,我们可以判断出四棱锥P-ABCD的底面是长为2,宽为1的矩形,高为
,代入棱锥体积公式即可得到四棱锥P-ABCD的体积;
(Ⅱ)P点在平面ABCD的射影为BC的中点O,连接OD,由三角形的中位线定理可得DE∥BO,DE=BO,进而可得OD∥BE,则∠PDO即为异面直线BE,PD所成角,解三角形即可得到答案.
(III)作CH⊥PD于H,连接EH,CE,我们可以得到∠EHC为二面角A-PD-C的平面角,解△CEH,即可得到二面角A-PD-C的正弦值.
| 2 |
(Ⅱ)P点在平面ABCD的射影为BC的中点O,连接OD,由三角形的中位线定理可得DE∥BO,DE=BO,进而可得OD∥BE,则∠PDO即为异面直线BE,PD所成角,解三角形即可得到答案.
(III)作CH⊥PD于H,连接EH,CE,我们可以得到∠EHC为二面角A-PD-C的平面角,解△CEH,即可得到二面角A-PD-C的正弦值.
解答: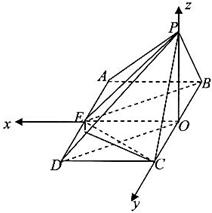 解:(I)由三视图可知四棱锥的高为
解:(I)由三视图可知四棱锥的高为
,
∴V=
•
•2•1=
(Ⅱ)由题意可知,P点在平面ABCD的射影为BC的中点O,连接OD
在矩形ABCD中,DE∥BO,且DE=BO∴OD∥BE,且OD=BE
∵异面直面BE,PD所成角等于PD于DO的所成角
∵PO⊥平面ABCD且PO=
∴∠POD=90°
又∵DC=CO=1,∠DCO=90°∴DO=
∴∠PDO=45°
∴异面直线BE,PD所成角的大小为45°
(Ⅲ)作CH⊥PD于H,连接EH,CE
又∵DE=DC,DH=DH
∴△EDH≌△CDH
∴∠EHD=∠CHD=90°,CH=EH=
=
=
∴EH⊥PD∴∠EHC为二面角A-PD-C的平面角
在△CEH中,cos∠EHC=
=-
∵∠EHC∈[0,π]∴sin∠EHC=
∴二面角A-PD-C的正弦值为
 解:(I)由三视图可知四棱锥的高为
解:(I)由三视图可知四棱锥的高为| 2 |
∴V=
| 1 |
| 3 |
| 2 |
2
| ||
| 3 |
(Ⅱ)由题意可知,P点在平面ABCD的射影为BC的中点O,连接OD
在矩形ABCD中,DE∥BO,且DE=BO∴OD∥BE,且OD=BE
∵异面直面BE,PD所成角等于PD于DO的所成角
∵PO⊥平面ABCD且PO=
| 2 |
又∵DC=CO=1,∠DCO=90°∴DO=
| 2 |
∴异面直线BE,PD所成角的大小为45°
(Ⅲ)作CH⊥PD于H,连接EH,CE
|
又∵DE=DC,DH=DH
∴△EDH≌△CDH
∴∠EHD=∠CHD=90°,CH=EH=
| DC•PC |
| PD |
1•
| ||
| 2 |
| ||
| 2 |
∴EH⊥PD∴∠EHC为二面角A-PD-C的平面角
在△CEH中,cos∠EHC=
| CH2+EH2-CE2 |
| 2CH•EH |
| 1 |
| 3 |
∵∠EHC∈[0,π]∴sin∠EHC=
2
| ||
| 3 |
∴二面角A-PD-C的正弦值为
2
| ||
| 3 |
点评:本题考查的知识点是二面角的平面角及求法,由三视图求体积,异面直线及其所成的角,其中(1)的关键是由三视图分析出几何体的形状及棱长,高等关键几何量,(2)的关键是构造∠PDO即为异面直线BE,PD所成角,(3)的关键是找到二面角A-PD-C的平面角∠EHC.

练习册系列答案
相关题目
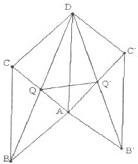 如图,矩形ABCD与矩形AB′C′D全等,且所在平面所成的二面角为a,记两个矩形对角线的交点分别为Q,Q′,AB=a,AD=b.
如图,矩形ABCD与矩形AB′C′D全等,且所在平面所成的二面角为a,记两个矩形对角线的交点分别为Q,Q′,AB=a,AD=b.