题目内容
【题目】在△ABC中,BC边上的中线AD长为3,且BD=2,sinB=![]() .
.
(Ⅰ)求sin∠BAD的值;
(Ⅱ)求AC的长.
【答案】(Ⅰ)![]() ;(Ⅱ)AC=4.
;(Ⅱ)AC=4.
【解析】试题分析:(1)在△ABD中,由正弦定理![]() 代入条件即可;
代入条件即可;
(2)在△ACD中,由余弦定理得:AC2=AD2+DC2-2ADDCcos∠ADC,只需依次确定边长和余弦值即可.
试题解析:
(1)在△ABD中,BD=2,sinB=![]() ,AD=3,
,AD=3,
∴由正弦定理 =
=![]() ,得sin∠BAD═
,得sin∠BAD═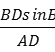 =
= =
=![]() ;
;
(2)∵sinB=![]() ,∴cosB=
,∴cosB=![]() ,
,
∵sin∠BAD=![]() ,∴cos∠BAD=
,∴cos∠BAD=![]() ,
,
∴cos∠ADC=cos(∠B+∠BAD)=![]() ×
×![]() -
-![]() ×
×![]() =-
=-![]() ,
,
∵D为BC中点,∴DC=BD=2,
∴在△ACD中,由余弦定理得:AC2=AD2+DC2-2ADDCcos∠ADC=9+4+3=16,
∴AC=4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】现从某班的一次期末考试中,随机的抽取了七位同学的数学(满分150分)、物理(满分110分)成绩如下表所示,数学、物理成绩分别用特征量![]() 表示,
表示,
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
t | 101 | 124 | 119 | 106 | 122 | 118 | 115 |
y | 74 | 83 | 87 | 75 | 85 | 87 | 83 |
求![]() 关于t的回归方程;
关于t的回归方程;
(2)利用(1)中的回归方程,分析数学成绩的变化对物理成绩的影响,并估计该班某学生数学成绩130分时,他的物理成绩(精确到个位).
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:

![]() .
. ![]()