题目内容
已知函数 (
(
 R).
R).
(1)当 时,求函数
时,求函数 的极值;
的极值;
(2)若函数 的图象与
的图象与 轴有且只有一个交点,求
轴有且只有一个交点,求 的取值范围.
的取值范围.
(1)当 时,
时,  取得极大值为
取得极大值为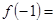
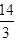 ;
;
当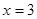 时,
时,  取得极小值为
取得极小值为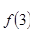
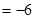 .
.
(2)a的取值范围是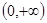 .
.
解析试题分析:(1)遵循“求导数,求驻点,讨论驻点两侧导数值符号,确定极值”.
(2)根据 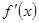 =
= 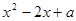 ,得到△=
,得到△= 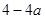 =
= 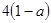 .
.
据此讨论:① 若a≥1,则△≤0,
此时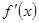 ≥0在R上恒成立,f(x)在R上单调递增 .
≥0在R上恒成立,f(x)在R上单调递增 .
计算f(0) ,
,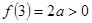 ,得到结论.
,得到结论.
② 若a<1,则△>0,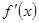 = 0有两个不相等的实数根,不妨设为
= 0有两个不相等的实数根,不妨设为 .
.
有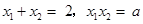 .
.
给出当 变化时,
变化时,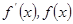 的取值情况表.
的取值情况表.
根据f(x1)·f(x2)>0, 解得a> .作出结论.
.作出结论.
试题解析: (1)当 时,
时,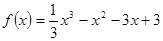 ,
,
∴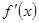
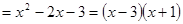 .
.
令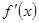 ="0," 得
="0," 得 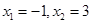 . 2分
. 2分
当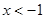 时,
时,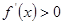 , 则
, 则 在
在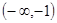 上单调递增;
上单调递增;
当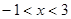 时,
时,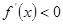 , 则
, 则 在
在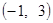 上单调递减;
上单调递减;
当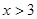 时,
时,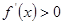 ,
,  在
在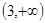 上单调递增. 4分
上单调递增. 4分
∴ 当 时,
时,  取得极大值为
取得极大值为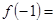
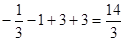 ;
;
当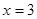 时,
时,  取得极小值为
取得极小值为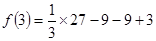
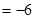 . 6分
. 6分
(2) ∵ 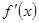 =
= 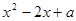 ,
,
∴△= 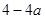 =
= 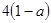 .
.
① 若a≥1,则△≤0, 7分
∴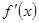 ≥0在R上恒成立,
≥0在R上恒成立,
∴ f(x)在R上单调递增 .
∵f(0) ,
,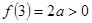 ,
,
∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点. 9分
② 若a<1,则△>0,
∴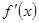 = 0有两个不相等的实数根,不妨设为
= 0有两个不相等的实数根,不妨设为 .
.
∴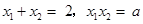 .
.
当 变化时,
变化时,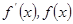 的取值情况如下表:
的取值情况如下表:x 
x1 (x1,x2)

萌齐小升初强化模拟训练系列答案
小升初全能卷系列答案
小升初全优模拟大考卷系列答案
考试先锋小升初全真模拟试卷系列答案
小升初衔接教材系列答案
学业水平总复习系列答案
毕业升学总动员系列答案
日练周测新语思英语系列答案
全优中考系统总复习系列答案
全优卷练考通系列答案
 对称,且f′(1)=0.
对称,且f′(1)=0.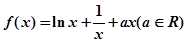
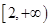 是单调减函数,求a的取值范围.
是单调减函数,求a的取值范围.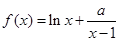 在
在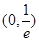 内有极值.
内有极值. 的取值范围;
的取值范围;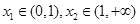 求证:
求证: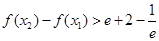 .
. (
(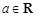 ).
).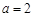 时,求
时,求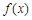 的图象在
的图象在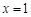 处的切线方程;
处的切线方程; 在
在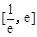 上有两个零点,求实数
上有两个零点,求实数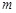 的取值范围;
的取值范围; 轴有两个不同的交点
轴有两个不同的交点 ,且
,且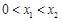 ,求证:
,求证: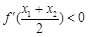 (其中
(其中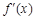 是
是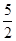 x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+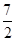 x2+ 1nx+b,(a,b为常数).
x2+ 1nx+b,(a,b为常数). ,
,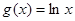 .
. 的极值;(2)若
的极值;(2)若 恒成立,求实数
恒成立,求实数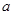 的值;
的值;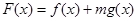
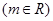 有两个极值点
有两个极值点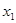 、
、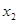 (
(
 的取值范围,并证明
的取值范围,并证明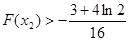 .
.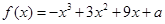 ,
,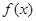 的单调递减区间;
的单调递减区间;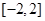 上的最大值为20,求它在该区间上的最小值.
上的最大值为20,求它在该区间上的最小值. 的定义域为
的定义域为 ,则
,则 ___________
___________