题目内容
设函数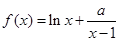 在
在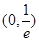 内有极值.
内有极值.
(1)求实数 的取值范围;
的取值范围;
(2)若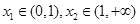 求证:
求证: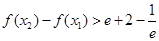 .
.
(1)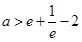 ;(2)证明见解析.
;(2)证明见解析.
解析试题分析:
解题思路:(1)利用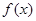 在
在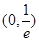 有极值
有极值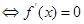 在
在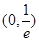 有解进行求解;
有解进行求解;
(2)要证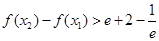 ,即证
,即证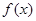 在
在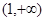 上是最小值与
上是最小值与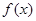 在
在 的最大值之差大于
的最大值之差大于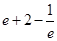 .
.
规律总结:利用导数研究函数的单调性、极值、最值及与函数有关的综合题,都体现了导数的重要性;此类问题往往从求导入手,思路清晰;但综合性较强,需学生有较高的逻辑思维和运算能力.
试题解析:(1)0<x<1或x>1时, 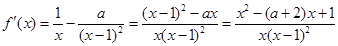
由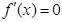 在
在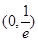 内有解,令
内有解,令 ,
,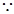
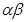 =1不妨设
=1不妨设 ,则
,则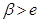 ,因
,因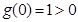 ,所以
,所以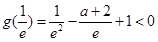 ,解得
,解得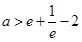
(2)证明:由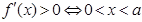 或
或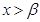 ,由
,由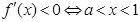 或
或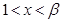 ,得
,得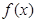 在
在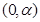 上单调递增,在
上单调递增,在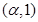 上单调递减,在
上单调递减,在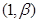 上单调递减,在
上单调递减,在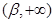 上单调递增.由
上单调递增.由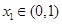 ,得
,得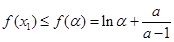 ,由
,由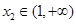 ,得
,得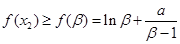 ,所以
,所以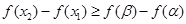 ,因为
,因为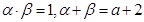 ,所以
,所以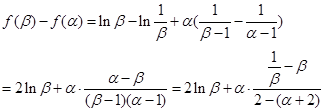

记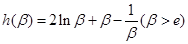
则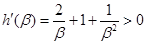 ,
,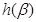 在
在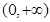 上单调递增,
上单调递增,
所以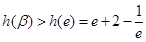
故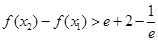 .
.
考点:利用导数研究函数的极值与最值.

练习册系列答案
相关题目
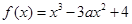 ,其中
,其中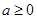 。
。 ,求函数
,求函数 的极值点和极值;
的极值点和极值;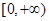 上的最小值。
上的最小值。 ,其中
,其中 ,
, 为自然对数的底数.
为自然对数的底数. 是函数
是函数 的导函数,求函数
的导函数,求函数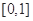 上的最小值;
上的最小值; ,函数
,函数 内有零点,求
内有零点,求 的取值范围。
的取值范围。 在
在 与
与 处都取得极值.
处都取得极值. 的解析式;
的解析式; (
(
 R).
R). 时,求函数
时,求函数 的极值;
的极值; 轴有且只有一个交点,求
轴有且只有一个交点,求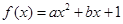 (
( 为实数,
为实数, ),
), ,⑴若
,⑴若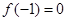 ,且函数
,且函数 的值域为
的值域为 ,求
,求 的表达式;
的表达式; ,且函数
,且函数 是否大0?
是否大0?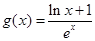 ,当
,当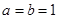 时,证明:对任意实数
时,证明:对任意实数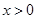 ,
, (其中
(其中 是
是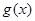 的导函数) .
的导函数) . 满足:①在
满足:①在 时有极值;②图像过点
时有极值;②图像过点 ,且在该点处的切线与直线
,且在该点处的切线与直线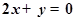 平行.
平行.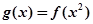 的单调递增区间.
的单调递增区间. 在
在 与
与 处都取得极值.
处都取得极值.  ,
, 的值;
的值; ,若对任意的
,若对任意的 ,总存在
,总存在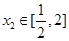 ,使得:
,使得: ,求实数
,求实数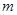 的取值范围.
的取值范围. 在点
在点 处的切线方程是
处的切线方程是