题目内容
【题目】在三棱锥A﹣BCD中,AB⊥平面BCD,BC⊥CD,且AB=3,BD=4,则三棱锥A﹣BCD外接球的半径为( )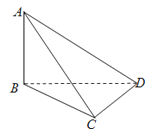
A.2
B.3
C.4
D.![]()
【答案】D
【解析】解:取AD的中点O,连结OB、OC
∵AB⊥平面BCD,CD平面BCD,∴AB⊥CD,
又∵BC⊥CD,AB∩BC=B,∴CD⊥平面ABC,
∵AC平面ABC,∴CD⊥AC,
∵OC是Rt△ADC的斜边上的中线,OC=![]() AD.
AD.
同理可得:Rt△ABD中,OB=![]() AD,
AD,
∴OA=OB=OC=OD=![]() AD,可得A、B、C、D四点在以O为球心的球面上.
AD,可得A、B、C、D四点在以O为球心的球面上.
Rt△ABD中,AB=3且BD=4,可得AD=![]() =5,
=5,
由此可得球O的半径R=![]() AD=
AD=![]() , 即三棱锥A﹣BCD外接球的半径为
, 即三棱锥A﹣BCD外接球的半径为![]() .
.
故选:D
【考点精析】解答此题的关键在于理解球内接多面体的相关知识,掌握球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长.

练习册系列答案
相关题目