��Ŀ����
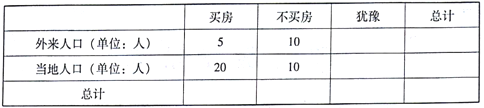
����Ŀ��ij������Ϊ�˶Է��ز��г����е��ؾ��ߣ�ͳ�Ʋ��Ŷ������˿ں͵����˿ڽ�����������Ԥ�ڵ��У��ü���������ķ�����ȡ��110�˽���ͳ�ƣ��õ���������������ȫ����
��֪�����������˿����뵱���˿���֮��Ϊ3:8.
��1����ȫ������������
��2���Ӳ�����е������˿����÷ֲ����������ȡ6�ˣ���һ��ͳ�������˿ڵ�ij������ָ�꣬��һ�����˵�ָ���Ϊ3��һ����ԥ�˵�ָ���Ϊ2��һ�������˵�ָ���Ϊ1�����ڴ���6���������ѡȡ3�ˣ���![]() ��ʾ��3��ָ��֮�ͣ���
��ʾ��3��ָ��֮�ͣ���![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
���𰸡���1����������2��![]()
�������������������1�����ݱ�����ϵ��ȷ�������˿����͵����˿����������ԥ������������ɣ���2����ȷ�����������ȡ���� ![]() ��������������ֱ����Ӧ���ʣ��б��ɵ÷ֲ��У���������ѧ������ʽ����ѧ����
��������������ֱ����Ӧ���ʣ��б��ɵ÷ֲ��У���������ѧ������ʽ����ѧ����
����������⣺�����������˿��к͵����˿��е���ԥ�����ֱ�Ϊ![]() �ˣ�
�ˣ� ![]() �ˣ���
�ˣ���
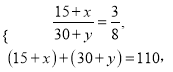 ���
���![]()
�� | ���� | ��ԥ | �ܼ� | |
�����˿ڣ���λ���ˣ� | 5 | 10 | 15 | 30 |
�����˿ڣ���λ���ˣ� | 20 | 10 | 50 | 80 |
�ܼ� | 25 | 20 | 65 | 110 |
���Ӳ�����е������˿����÷ֲ����������ȡ��![]() ���У���1�ˣ�����2�ˣ���ԥ3�ˣ�����
���У���1�ˣ�����2�ˣ���ԥ3�ˣ�����![]() �����п���ȡֵΪ
�����п���ȡֵΪ![]() ��
��
![]() ��
�� ![]() ��
��
![]() ��
�� ![]() ��
��
����![]() �ķֲ���Ϊ
�ķֲ���Ϊ
X | 7 | 6 | 5 | 4 |
P |
|
|
|
|
����![]() ����ѧ������
����ѧ������![]() ��
��