题目内容
已知集合
 ,若该集合具有下列性质的子集:每个子集至少含有2个元素,且每个子集中任意两个元素之差的绝对值大于1,则称这些子集为
,若该集合具有下列性质的子集:每个子集至少含有2个元素,且每个子集中任意两个元素之差的绝对值大于1,则称这些子集为 子集,记
子集,记 子集的个数为
子集的个数为 .
.
(1)当 时,写出所有
时,写出所有 子集;
子集;
(2)求 ;
;
(3)记 ,求证:
,求证:
(1) ;(2)133;(3)详见解析
;(2)133;(3)详见解析
解析试题分析:(1)当 子集中只含有2个元素时,含1时,另一个元素只能是3或4或5;含2时另一个元素只能是4或5;含3时另一个元素只能是5;当
子集中只含有2个元素时,含1时,另一个元素只能是3或4或5;含2时另一个元素只能是4或5;含3时另一个元素只能是5;当 子集中含3个元素时只能是1、3、5这三个元素。(2)应先求关于
子集中含3个元素时只能是1、3、5这三个元素。(2)应先求关于 的解析式:
的解析式: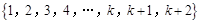 的
的 子集可分为两类:第一类子集中不含有
子集可分为两类:第一类子集中不含有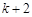 ,相当于
,相当于 的
的 子集个数
子集个数 ;第二类子集中含有
;第二类子集中含有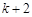 则肯定不含
则肯定不含 ,相当于
,相当于 的
的 子集个数
子集个数 和
和 的单元素与元素
的单元素与元素 构成的集合数
构成的集合数 ,即
,即 ,分析可知
,分析可知 ,则可求
,则可求 。(3)可用错位相减法证明。
。(3)可用错位相减法证明。
解:(1)当 时,所以
时,所以 子集:
子集: ,
, ,
, ,
,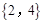 ,
, ,
,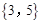 ,
, .
.
(2)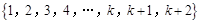 的
的 子集可分为两类:第一类子集中不含有
子集可分为两类:第一类子集中不含有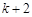 ,这类子集有
,这类子集有 个;
个;
第二类子集中含有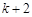 ,这类子集成为
,这类子集成为 的
的 子集与
子集与 的并,或
的并,或 的单元素子集与
的单元素子集与 的并,共有
的并,共有 个.
个.
所以 .
.
因为 ,
, ,
,
所以 ,
, ,
,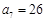 ,
, ,
, ,
, .
.
(3)因为 , ①
, ①
所以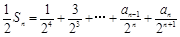 ②
②
① ②得
②得



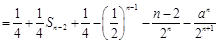


所以 .
.
考点:新概念问题。

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 中,
中,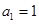 ,
, ,其通项公式
,其通项公式 = .
= . ,且
,且 按某种顺序排列成等差数列.
按某种顺序排列成等差数列. 的值;
的值; 的首项和公差都为
的首项和公差都为 的首项和公比都为
的首项和公比都为 项和分别为
项和分别为 ,且
,且 ,求满足条件的自然数
,求满足条件的自然数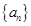 的前三项分别为
的前三项分别为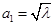 ,
, ,
,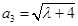 ,(其中
,(其中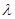 为正常数)。设
为正常数)。设
 。
。 的值;
的值;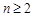 时,
时,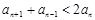 .
. =
= ,求
,求 的值;
的值;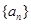 中,
中,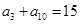 ,且
,且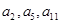 成等比数列.
成等比数列.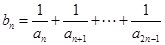 ,证明:
,证明: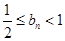 .
.
 的前
的前 项和为
项和为 ,满足:
,满足:
 .递增的等比数列
.递增的等比数列 前
前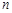 项和为
项和为 ,满足:
,满足: .
. 对
对 ,均有
,均有 成立,求
成立,求 .
.