题目内容
若点P在以F1,F2为焦点的椭圆上,PF2⊥F1F2,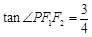 ,则椭圆的离心率为___________
,则椭圆的离心率为___________
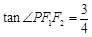 ,则椭圆的离心率为___________
,则椭圆的离心率为___________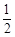
因为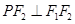 ,所以在
,所以在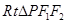 中,因为
中,因为 ,所以
,所以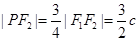 。因为
。因为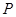 点在椭圆上,所以
点在椭圆上,所以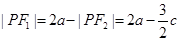 。由
。由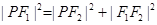 可得,
可得,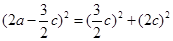 ,化简可得
,化简可得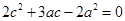 ,解得
,解得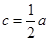 或
或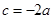 (舍),故
(舍),故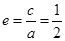
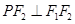 ,所以在
,所以在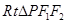 中,因为
中,因为 ,所以
,所以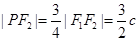 。因为
。因为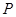 点在椭圆上,所以
点在椭圆上,所以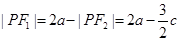 。由
。由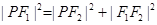 可得,
可得,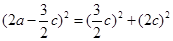 ,化简可得
,化简可得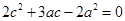 ,解得
,解得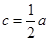 或
或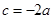 (舍),故
(舍),故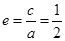

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
题目内容
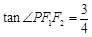 ,则椭圆的离心率为___________
,则椭圆的离心率为___________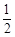
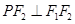 ,所以在
,所以在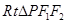 中,因为
中,因为 ,所以
,所以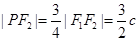 。因为
。因为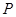 点在椭圆上,所以
点在椭圆上,所以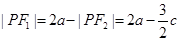 。由
。由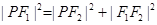 可得,
可得,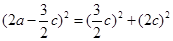 ,化简可得
,化简可得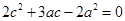 ,解得
,解得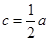 或
或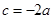 (舍),故
(舍),故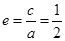

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案