Question

【题目】已知函数，g(x)＝－x2＋2bx－4，若对任意的x1∈(0，2)，任意的x2∈[1，2]，不等式f(x1)≥g(x2)恒成立，则实数b的取值范围是(　　)

A. B. (1，＋∞)

C. D.

Answer 1

【答案】A

【解析】依题意，问题等价于f(x1)min≥g(x2)max.

(x＞0)，

所以.

由f′(x)＞0，解得1＜x＜3，故函数f(x)的单调递增区间是(1，3)，同理得f(x)的单调递减区间是(0，1)和(3，＋∞)，故在区间(0，2)上，x＝1是函数f(x)的极小值点，这个极小值点是唯一的，所以f(x1)min＝f(1)＝－.

函数g(x2)＝－＋2bx2－4，x2∈[1，2].

当b＜1时，g(x2)max＝g(1)＝2b－5；

当1≤b≤2时，g(x2)max＝g(b)＝b2－4；

当b＞2时，g(x2)max＝g(2)＝4b－8.

故问题等价于

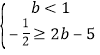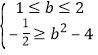或或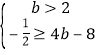

解第一个不等式组得b＜1，

解第二个不等式组得1≤b≤，

第三个不等式组无解.

综上所述，b的取值范围是.

故选A.