题目内容
在△ABC中，下列命题中正确的有：
①
-
=
；
②若
•
＞0，则△ABC为锐角三角形；
③O是△ABC所在平面内一定点，动点P满足
=
+λ(
+
)，λ∈[0，+∞），则动点P一定过△ABC的重心；
④O是△ABC内一定点，且
+
+2
=
，则
=
；
⑤若（
+
）•
=0，且
•
=
，则△ABC为等边三角形．
③⑤
③⑤
①
| AB |
| AC |
| BC |
②若
| AC |
| AB |
③O是△ABC所在平面内一定点，动点P满足
| OP |
| 0A |
| AB |
| AC |
④O是△ABC内一定点，且
| OA |
| OC |
| OB |
| 0 |
| S△AOC |
| S△ABC |
| 1 |
| 3 |
⑤若（
| ||
丨
|
| ||
丨
|
| BC |
| ||
丨
|
| ||
丨
|
| 1 |
| 2 |
分析：根据平面向量的有关概念以及平面向量的数量积以及数量积的应用分别进行判断．
解答：解：①
-
=
．∴①错误．
②若
•
＞0，则A为锐角，但无法确定B，C的大小，∴△ABC为锐角三角形不正确，∴②错误．
③由动点P满足
=
+λ(
+
)，得
=λ(
+
)，即Ap过△ABC的中线，∴P过△ABC的重心．∴③正确．
④解：设D为AC中点，连结OD，则OD是△OBC的中线，
∴向量
=
(
+
)
∵由已知且
+
+2
=
得
=-
(
+
)，
∴向量因
=-
=
，
即B、O、D三点共线，且O为BD的中点
∴△ABD中，AO是BD边上的中线，可得S△OAB=S△OAD．
同理可得△BCD中，S△OBC=S△OCD，
∴S△OAB=S△OBC=S△OAD=S△OCD=S△OAC
由此可得S△OAB：S△OBC：S△OAC=1：1：2，
∴S△AOC：S△ABC=2：4=1：2=
，∴④错误．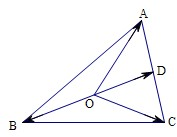
⑤由（
+
）•
=0，可知角A的角平分线垂直于BC，
∴AB=AC．
由
•
=
，可得cosA=
，解得A=
，
∴△ABC为等边三角形，∴⑤正确．
故答案为：③⑤．
| AB |
| AC |
| CB |
②若
| AC |
| AB |
③由动点P满足
| OP |
| 0A |
| AB |
| AC |
| AP |
| AB |
| AC |
④解：设D为AC中点，连结OD，则OD是△OBC的中线，
∴向量
| OD |
| 1 |
| 2 |
| OA |
| OC |
∵由已知且
| OA |
| OC |
| OB |
| 0 |
| OB |
| 1 |
| 2 |
| OA |
| OC |
∴向量因
| OD |
| OB |
| BO |
即B、O、D三点共线，且O为BD的中点
∴△ABD中，AO是BD边上的中线，可得S△OAB=S△OAD．
同理可得△BCD中，S△OBC=S△OCD，
∴S△OAB=S△OBC=S△OAD=S△OCD=S△OAC
由此可得S△OAB：S△OBC：S△OAC=1：1：2，
∴S△AOC：S△ABC=2：4=1：2=
| 1 |
| 2 |
⑤由（
| ||
丨
|
| ||
丨
|
| BC |
∴AB=AC．
由
| ||
丨
|
| ||
丨
|
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
∴△ABC为等边三角形，∴⑤正确．
故答案为：③⑤．
点评：本题主要考查平面向量有关概念和数量积的应用，要求熟练掌握数量积的应用，比较综合．
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
，若函数y=f（x）在[0，1]上为单调递减函数，则下列命 题正确的是（ ）