题目内容
已知:圆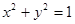 过椭圆
过椭圆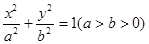 的两焦点,与椭圆有且仅有两个公共点:直线
的两焦点,与椭圆有且仅有两个公共点:直线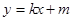 与圆
与圆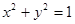 相切 ,与椭圆
相切 ,与椭圆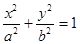 相交于A,B两点记
相交于A,B两点记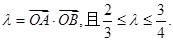
(Ⅰ)求椭圆的方程;
(Ⅱ)求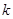 的取值范围;
的取值范围;
(Ⅲ)求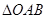 的面积S的取值范围.
的面积S的取值范围.
(1)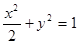
(2)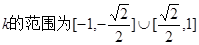
(3)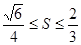
解析试题分析:解:(Ⅰ)由题意知2c="2,c=1" , 因为圆与椭圆有且只有两个公共点,从而b=1.故a=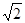
所求椭圆方程为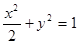 3分
3分
(Ⅱ)因为直线l:y=kx+m与圆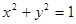 相切
相切
所以原点O到直线l的距离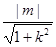 =1,即:m
=1,即:m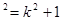 5分
5分
又由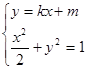 ,(
,(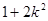 )
)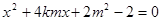
设A(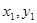 ),B(
),B(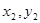 ),则
),则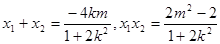 7分
7分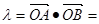
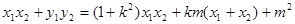 =
=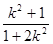 ,由
,由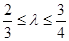 ,故
,故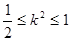 ,
,
即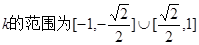 9分
9分
(III)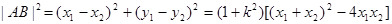
= ,由
,由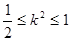 ,得:
,得: 11分
11分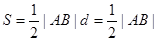 ,所以:
,所以: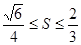 12分
12分
考点:直线与椭圆的位置关系
点评:主要是考查了椭圆方程的求解,以及直线与椭圆的位置关系的运用,属于中档题。

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
 -6x+1与坐标轴的交点都在圆C上.
-6x+1与坐标轴的交点都在圆C上.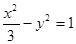 与抛物线
与抛物线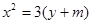 相交于
相交于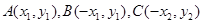
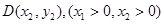 ,直线AC、BD的交点为P(0,p)。
,直线AC、BD的交点为P(0,p)。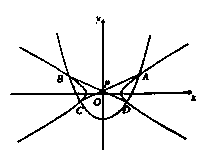
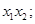
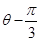 )=1,M,N分别为C与x轴,y轴的交点。
)=1,M,N分别为C与x轴,y轴的交点。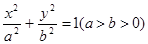 的左焦点为
的左焦点为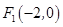 ,直线
,直线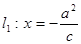 与
与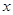 轴交于点
轴交于点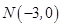 ,过点
,过点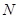 且倾斜角为30°的直线
且倾斜角为30°的直线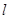 交椭圆于
交椭圆于 两点.
两点. 在以线段
在以线段 为直径的圆上;
为直径的圆上;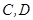 ,以
,以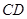 为直径且过点
为直径且过点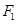 的所有圆中,求面积最小的圆的半径长.
的所有圆中,求面积最小的圆的半径长.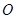 与离心率为
与离心率为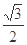 的椭圆
的椭圆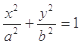 (
(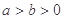 )相切于点
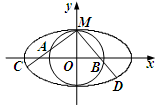
)相切于点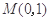 .
.
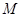 引两条互相垂直的两直线
引两条互相垂直的两直线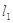 、
、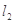 与两曲线分别交于点
与两曲线分别交于点 、
、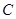 与点
与点 、
、 (均不重合).
(均不重合).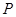 为椭圆上任一点,记点
为椭圆上任一点,记点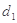 、
、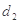 ,求
,求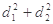 的最大值;
的最大值;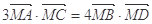 ,求
,求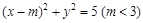 与椭圆E:
与椭圆E: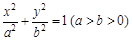 有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
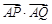 的取值范围.
的取值范围.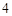 的双曲线的焦点在x轴上,且过点P
的双曲线的焦点在x轴上,且过点P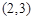 .
.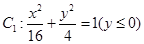 ,曲线
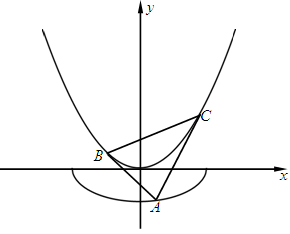
,曲线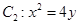 .自曲线
.自曲线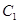 上一点
上一点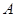 作
作 的两条切线切点分别为
的两条切线切点分别为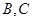 .
.
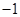 ,求
,求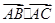 ;
;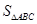 的最大值.
的最大值.